题目内容
10.设数列{an}满足an=2an-1+n(n≥2且n∈N*),{an}的前n项和为Sn,数列{bn}满足bn=an+n+2.(1)若a1=1,求Sn;
(2)试判断数列{bn}是否为等比数列?请说明理由.
分析 (1)由数列{an}满足an=2an-1+n(n≥2且n∈N*),变形为an+n+2=2(an-1+n+1),利用等比数列的通项公式可得an,再利用等比数列与等差数列的前n项和公式即可得出.
(2)由(1)利用等比数列的定义即可得出.
解答 解:(1)∵数列{an}满足an=2an-1+n(n≥2且n∈N*),
∴an+n+2=2(an-1+n+1),
∴数列{an+n+2}是等比数列,首项为4,公比为2.
∴an+n+2=4×2n-1.
∴an=2n+1-(n+2).
∴Sn=$\frac{{4×(2}^{n+1}-1)}{2-1}$-$\frac{n(3+n+2)}{2}$
=2n+3-4-$\frac{n(n+5)}{2}$.
(2)∵bn=an+n+2,∴bn+1=an+1+n+3.
由(1)可得:bn+1=2bn.
∴数列{bn}为等比数列,首项为4,公比为2.
点评 本题考查了等比数列与等差数列的定义通项公式前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.函数y=$\frac{\sqrt{1-x}}{2{x}^{2}-3x-2}$的定义域是( )
| A. | (-∞,1] | B. | (-∞,2] | C. | (-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,2) | D. | (-∞,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1] |
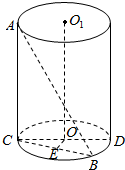 如图,AC为圆柱的母线,CD为底面直径,线段AB的两个端点分别在上、下底面圆周上,它与圆周的轴OO1之间的距离为3,所成角为30°,且AB=16,求此圆柱的侧面积.
如图,AC为圆柱的母线,CD为底面直径,线段AB的两个端点分别在上、下底面圆周上,它与圆周的轴OO1之间的距离为3,所成角为30°,且AB=16,求此圆柱的侧面积.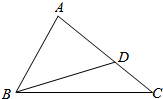 如图,△ABC中,∠B满足$\sqrt{2}$sinB-cosB=1,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$.
如图,△ABC中,∠B满足$\sqrt{2}$sinB-cosB=1,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{4\sqrt{3}}{3}$.