题目内容
10.设函数f(x)=log3(9-x2)的定义域为(-3,3),值域为(-∞,2),不等式f(x)>1的解集为($-\sqrt{6},\sqrt{6}$).分析 根据对数函数的性质,求定义域以及值域;利用对数函数的单调性求不等式的解集.
解答 解:要使函数f(x)=log3(9-x2)有意义,只要9-x2>0m解得-3<x<3,即函数定义域为(-3,3);
而由0<9-x2<9,所以log3(9-x2)的范围为(-∞,2),即函数值域为(-∞,2),
不等式f(x)>1为log3(9-x2)>1,即9-x2>3,解得$-\sqrt{6}$<x<$\sqrt{6}$;
故答案为:(-3,3);(-∞,2);($-\sqrt{6},\sqrt{6}$).
点评 本题考查了对数函数的性质以及对数不等式的解法;用到了对数函数的单调性以及logaa=1.

练习册系列答案
相关题目
15.设0<b<a<1,则下列不等式不成立的是( )
| A. | 2b<2a<2 | B. | $0<{log_{\frac{1}{2}}}a<{log_{\frac{1}{2}}}$b | ||
| C. | ab<b2<1 | D. | ab<a2<1 |
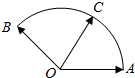 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°.点C在以OA,OB为半径的圆弧上,∠AOC=30°如图所示,若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x=$\frac{2\sqrt{3}}{3}$;y=$\frac{\sqrt{3}}{3}$.
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°.点C在以OA,OB为半径的圆弧上,∠AOC=30°如图所示,若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x=$\frac{2\sqrt{3}}{3}$;y=$\frac{\sqrt{3}}{3}$. 设△ABC的内角A、B、C所对的边分别为a、b、c,$\frac{5(sinA-sinC)}{sin(A+C)}=\frac{5sinB-8sinC}{sinA+sinC}$,点P为△ABC内任意一点,点P到三边的距离之和为d.
设△ABC的内角A、B、C所对的边分别为a、b、c,$\frac{5(sinA-sinC)}{sin(A+C)}=\frac{5sinB-8sinC}{sinA+sinC}$,点P为△ABC内任意一点,点P到三边的距离之和为d.