题目内容
20．已知f（x）为偶函数，f（1）=9，f（x-1）为奇函数，求f（9）．分析 根据题意和函数的奇偶性的性质通过化简、变形，求出函数的周期，利用函数的周期性求出f（9）的值．
解答 解：由题意得，f（x）为偶函数，f（x-1）为奇函数，
∴f（x-1）=-f（-x-1），则f（x-2）=-f（-x）=-f（x），即f（x+2）=-f（x），
∴f（x+4）=-f（x+2）=f（x），
则偶函数f（x）是以4为周期的周期函数，
又f（1）=9，则f（9）=f（8+1）=f（1）=9．
点评 本题考查函数的奇偶性和周期性的综合应用，考查化简、变形能力，属于基础题．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
11．与直线x-y+4=0和圆x2+y2-2x+2y=0都相切的半径最小的圆的方程是（ ）
| A． | （x+1）2+（y+1）2=2 | B． | （x+1）2+（y-1）2=2 | C． | （x+1）2+（y+1）2=4 | D． | （x+1）2+（y-1）2=4 |
8．
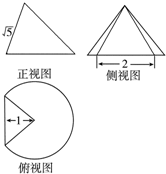一个圆锥被过顶点的平面截去了较小的一部分，余下的几何体的三视图如图，则该几何体的表面积为（ ）
一个圆锥被过顶点的平面截去了较小的一部分，余下的几何体的三视图如图，则该几何体的表面积为（ ）| A． | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{3π}{2}$+1 | B． | 2$\sqrt{5}$+3$\sqrt{3}$π+$\frac{3π}{2}$+1 | C． | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{3π}{2}$ | D． | $\sqrt{5}$+$\frac{3\sqrt{3}π}{2}$+$\frac{π}{2}$+1 |
12．已知α，β都是锐角，sinα=$\frac{1}{2}$，cosβ=$\frac{1}{2}$，则sin（α+β）=（ ）
| A． | 1 | B． | $\frac{{\sqrt{3}}}{2}$ | C． | -1 | D． | $\frac{{\sqrt{3}-1}}{2}$ |