Question

20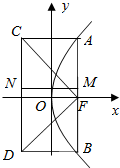．如图，已知抛物线方程y²=2px（p＞0），AB是过焦点F的一条弦，点A（x₁，y₁），B（x₂，y₂）．求证：
（1）y₁y₂=-p²，x₁x₂=$\frac{{p}^{2}}{4}$；
（2）|AB|=x₁+x₂+p=$\frac{2p}{si{n}^{2}θ}$（θ为直线AB的倾斜角）．

Answer 1

分析 （1）设直线AB的方程为x=my+$\frac{p}{2}$，代入y²=2px，再利用韦达定理，即可得到结论；
（2）利用抛物线的定义，可得|AB|=x₁+x₂+p；结合y₁y₂=-p²，进一步得到|AB|=x₁+x₂+p=$\frac{2p}{si{n}^{2}θ}$．

解答 证明：（1）设直线AB的方程为x=my+$\frac{p}{2}$，代入y²=2px，可得y²-2pmy-p²=0，
∴y₁y₂=-p²，∴x₁x₂=$\frac{（{y}_{1}{y}_{2}）^{2}}{4{p}^{2}}=\frac{{p}^{4}}{4{p}^{2}}=\frac{{p}^{2}}{4}$；
（2）∵AB是过抛物线y²=2px（p＞0）的焦点的弦，
∴由抛物线定义可得|AB|=x₁+$\frac{p}{2}$+x₂+$\frac{p}{2}$=x₁+x₂+p；
由（1）知，y₁y₂=-p²，y₁+y₂=2pm，
∴${{y}_{1}}^{2}+{{y}_{2}}^{2}$=（y₁+y₂）²-2y₁y₂=4p²m²+2p²，
又${{y}_{1}}^{2}+{{y}_{2}}^{2}$=2p（x₁+x₂）=4p²m²+2p²，∴x₁+x₂=2pm²+p，
∴θ=90°时，m=0，∴|AB|=2p=$\frac{2p}{si{n}^{2}θ}$；θ≠90°时，m=$\frac{1}{tanθ}$，|AB|=$\frac{2p}{ta{n}^{2}θ}$+2p=$\frac{2p}{si{n}^{2}θ}$．
∴|AB|=x₁+x₂+p=$\frac{2p}{si{n}^{2}θ}$．

点评 本题考查直线与抛物线的位置关系，考查韦达定理的运用，考查弦长的计算，属于中档题