题目内容
9.已知函数f(x)=$\frac{{x}^{2}-1}{{x}^{2}}$.(1)证明f(x)为偶函数;
(2)若不等式k≤xf(x)+$\frac{1}{x}$在x∈[1,3]上恒成立,求实数k的取值范围;
(3)当x∈[$\frac{1}{m}$,$\frac{1}{n}$](m>0,n>0)时,函数g(x)=tf(x)+1,(t≥0)的值域为[2-3m,2-3n],求实数t的取值范围.
分析 (1)利用定义判断函数的奇偶性,先求定义域,再判断f(-x)=$\frac{{x}^{2}-1}{{x}^{2}}$=f(x);
(2)直接求右表达式的最小值即可;
(3)得出g(x)=tf(x)+1=t(1-$\frac{1}{{x}^{2}}$)+1 (t≥0)在x∈[$\frac{1}{m}$,$\frac{1}{n}$]上递增,可得出g($\frac{1}{m}$)=2-3m,g($\frac{1}{n}$)=2-3n,
构造一方程m,n是t(1-x2)=2-3x的两个不相等的正跟,利用二次函数和韦达定理得出t的范围.
解答 (1)证明:函数的定义域为(-∞,0)∪(0,+∞)关于原点对称,
∵f(-x)=$\frac{{x}^{2}-1}{{x}^{2}}$=f(x),
∴f(x)为偶函数;
(2)k≤xf(x)+$\frac{1}{x}$=x在x∈[1,3]上恒成立,
∴k≤1;
(3)g(x)=tf(x)+1=t(1-$\frac{1}{{x}^{2}}$)+1 (t≥0)在x∈[$\frac{1}{m}$,$\frac{1}{n}$]上递增,
∴g($\frac{1}{m}$)=2-3m,g($\frac{1}{n}$)=2-3n,
∴t(1-m2)+1=2-3m,t(1-n2)+1=2-3n,
∴m,n是t(1-x2)+1=2-3x的两个不相等的正跟,
∴tx2-3x+1-t=0(t>0),
∴△=9-4t(1-t)>0,
$\frac{3}{t}$>0,
$\frac{1-t}{t}$>0,
∴0<t<1.
点评 考查了奇偶性的判断和恒成立问题的转换,利用构造方程的思想,通过韦达定理得出参数t的范围.

练习册系列答案
相关题目
19.若关于x的方程2ax2-x+2a-1=0的两根均为正实数,则实数a的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | (-∞,0)∪($\frac{1}{2}$,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | ($\frac{1}{2}$,$\frac{\sqrt{2}+1}{4}$] |
17.不等式tanx>a在x∈(-$\frac{π}{4},\frac{π}{2}$)上恒成立,则a的取值范围( )
| A. | a>1 | B. | a≤1 | C. | a<-1 | D. | a≤-1 |
4.已知{$\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$}是空间的一个单位正交基地,且$\overrightarrow{OA}=\overrightarrow{i}+3\overrightarrow{k}$,$\overrightarrow{OB}=2\overrightarrow{j}$,则△OAB(O为坐标原点)的面积是( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\sqrt{10}$ | C. | $\frac{\sqrt{35}}{2}$ | D. | $\sqrt{35}$ |
19.已知a,b∈R,a2+2b2=1,则a-b的最小值为( )
| A. | -$\sqrt{5}$ | B. | -$\frac{\sqrt{6}}{2}$ | C. | -$\sqrt{6}$ | D. | -$\sqrt{2}$ |
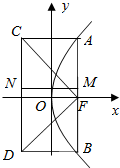 如图,已知抛物线方程y2=2px(p>0),AB是过焦点F的一条弦,点A(x1,y1),B(x2,y2).求证:
如图,已知抛物线方程y2=2px(p>0),AB是过焦点F的一条弦,点A(x1,y1),B(x2,y2).求证: