题目内容

11．函数f（x）=|ax2+bx+c|（a≠0）的定义域分成四个单调区间的充要条件是 （　　）
A．a＞0且b2-4ac＞0B．-$\frac{b}{2a}$＞0C．b2-4ac＞0D．-$\frac{b}{2a}＜0$

分析 分情况作出y=ax2+bx+c的图象，然后将图象x轴下方的图象翻折到x轴上边得出f（x）的图象，结合图象即可选出答案．

解答 解：当△=b2-4ac＞0时，y=ax2+bx+c图象与x轴交于两点，然后将图象x轴下方的图象翻折到x轴上边即可得出f（x）的图象，如图1；
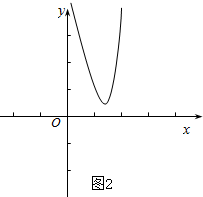
当△=b2-4ac＜0时，y=ax2+bx+c图象与x轴无交点，然后将图象x轴下方的图象翻折到x轴上边即可得出f（x）的图象，如图2；
当△=b2-4ac=0时，y=ax2+bx+c图象与x轴交与一点，然后将图象x轴下方的图象翻折到x轴上边即可得出f（x）的图象，如图3；
故选C．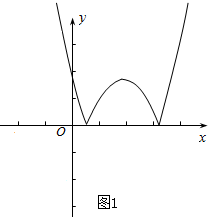

点评 本题考查了二次函数的图象，图象变换，数形结合解题思想．属于中档题．

练习册系列答案
相关题目
1．已知f（x）=log2x，g（x）=lgx．
（1）当x为何值时，f（x）=g（x）？
（2）当x为何值时，f（x）＞1？
（3）当x为何值时，0＜g（x）＜1？
2．与圆x2+y2-10x-8y+25=0相内切，且与两条坐标轴都相切的圆的方程为（x-5）2+（y-5）2=25．
19．若关于x的方程2ax2-x+2a-1=0的两根均为正实数，则实数a的取值范围是（　　）
A．（0，$\frac{1}{2}$）B．（-∞，0）∪（$\frac{1}{2}$，+∞）C．（$\frac{1}{2}$，+∞）D．（$\frac{1}{2}$，$\frac{\sqrt{2}+1}{4}$]
6．设f（x）是任意一个函数，其定义域在x轴上关于原点对称
（1）判断下列函数的奇偶性：F（x）=$\frac{1}{2}$[f（x）+f（-x）]，G（x）=$\frac{1}{2}$[f（x）-f（-x）]；
（2）求证：f（x）一定可以表示成一个奇函数与一个偶函数的和．
16．已知10α=2，10β=3，求100${\;}^{2α-\frac{1}{3}β}$．
3．设f′（x）=k，求$\underset{lim}{x→∞}$[f（x+a）-f（x）]．
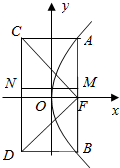20．如图，已知抛物线方程y2=2px（p＞0），AB是过焦点F的一条弦，点A（x1，y1），B（x2，y2）．求证：
（1）y1y2=-p2，x1x2=$\frac{{p}^{2}}{4}$；
（2）|AB|=x1+x2+p=$\frac{2p}{si{n}^{2}θ}$（θ为直线AB的倾斜角）．
1．点（$\sqrt{2}$，2）在幂函数f（x）的图象上，点（-2，$\frac{1}{4}$）在幂函数g（x）的图象上．
（1）判断f（x）与g（x）的奇偶性；
（2）设h（x）=（$\frac{1}{3}$）f（x），是否存在x1∈R，x2∈（0，1]，使h（x1）=g（x2）？若存在，求x1，x2的值；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网