题目内容
15.已知圆的方程是x2+y2=2,它截直线y=x+1所得的弦长是$\sqrt{6}$.分析 由已知中直线方程和圆的方程,求出圆x2+y2=2的圆心O(0,0)到直线y=x+1的距离d,圆的半径r,代入弦长公式可得答案.
解答 解:圆x2+y2=2的圆心O(0,0)到直线y=x+1,即x-y+1=0的距离d=$\frac{1}{\sqrt{2}}$,
圆x2+y2=2的半径r=$\sqrt{2}$,
则直线y=x+1被圆x2+y2=2截得的弦长l=2$\sqrt{2-\frac{1}{2}}$=$\sqrt{6}$,
故答案为:$\sqrt{6}$.
点评 本题考查的知识点是直线与圆的位置关系,其中熟练掌握圆的弦长公式是解答的关键.

练习册系列答案
相关题目
10.已知直线l的斜率k=2,并且经过一点(2,-3)则直线的点斜式方程为( )
| A. | y-3=2(x-2) | B. | y+3=2(x-2) | C. | y-2=k(x+3) | D. | y-2=2(x-3) |
7. 若某几何体的三视图如图所示,其中A1M:AM=7:5.则此几何体的体积等于( )
若某几何体的三视图如图所示,其中A1M:AM=7:5.则此几何体的体积等于( )
 若某几何体的三视图如图所示,其中A1M:AM=7:5.则此几何体的体积等于( )
若某几何体的三视图如图所示,其中A1M:AM=7:5.则此几何体的体积等于( )| A. | 55 | B. | 62 | C. | 65 | D. | 72 |
4.已知{$\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$}是空间的一个单位正交基地,且$\overrightarrow{OA}=\overrightarrow{i}+3\overrightarrow{k}$,$\overrightarrow{OB}=2\overrightarrow{j}$,则△OAB(O为坐标原点)的面积是( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\sqrt{10}$ | C. | $\frac{\sqrt{35}}{2}$ | D. | $\sqrt{35}$ |
5.利用正弦线比较sin1,sin1.2,sin1.5的大小关系是( )
| A. | sin1>sin1.2>sin1.5 | B. | sin1>sin1.5>sin1.2 | ||
| C. | sin1.5>sin1.2>sin1 | D. | sin1.2>sin1>sin1.5 |
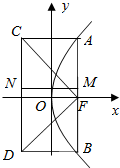 如图,已知抛物线方程y2=2px(p>0),AB是过焦点F的一条弦,点A(x1,y1),B(x2,y2).求证:
如图,已知抛物线方程y2=2px(p>0),AB是过焦点F的一条弦,点A(x1,y1),B(x2,y2).求证: