题目内容
5.证明:$\sqrt{ab}$≥$\frac{2ab}{a+b}$.分析 根据基本不等式,分析法可证.
解答 证明:要证:$\sqrt{ab}$≥$\frac{2ab}{a+b}$,
只要证1≥$\frac{2\sqrt{ab}}{a+b}$,
只要证2$\sqrt{ab}$≤a+b,
由基本不等式可得2$\sqrt{ab}$≤a+b显然成立,
所以$\sqrt{ab}$≥$\frac{2ab}{a+b}$.
点评 本题考查不等式的证明,涉及基本不等式和分析法证明不等式,属基础题.

练习册系列答案
相关题目
13.已知两点P(1,3)Q(4,-1),则这两点间的距离为( )
| A. | 35 | B. | 25 | C. | 15 | D. | 5 |
17.不等式tanx>a在x∈(-$\frac{π}{4},\frac{π}{2}$)上恒成立,则a的取值范围( )
| A. | a>1 | B. | a≤1 | C. | a<-1 | D. | a≤-1 |
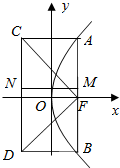 如图,已知抛物线方程y2=2px(p>0),AB是过焦点F的一条弦,点A(x1,y1),B(x2,y2).求证:
如图,已知抛物线方程y2=2px(p>0),AB是过焦点F的一条弦,点A(x1,y1),B(x2,y2).求证: