题目内容
10.点A(2,-1)与B(4,3)的中点坐标是(3,1).分析 设A、B的中点为M,其坐标为(x,y),由中点坐标公式可得$\left\{\begin{array}{l}{x=\frac{2+4}{2}}\\{y=\frac{(-1)+3}{2}}\end{array}\right.$,解可得x、y的值,即可得答案.
解答 解:设A、B的中点为M,其坐标为(x,y),
根据题意,有$\left\{\begin{array}{l}{x=\frac{2+4}{2}}\\{y=\frac{(-1)+3}{2}}\end{array}\right.$,解可得$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$;
即点M的坐标为(3,1);
故答案为(3,1).
点评 本题考查中点坐标公式的运用,牢记中点坐标公式的形式即可.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
19.若关于x的方程2ax2-x+2a-1=0的两根均为正实数,则实数a的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | (-∞,0)∪($\frac{1}{2}$,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | ($\frac{1}{2}$,$\frac{\sqrt{2}+1}{4}$] |
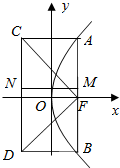 如图,已知抛物线方程y2=2px(p>0),AB是过焦点F的一条弦,点A(x1,y1),B(x2,y2).求证:
如图,已知抛物线方程y2=2px(p>0),AB是过焦点F的一条弦,点A(x1,y1),B(x2,y2).求证: