题目内容
设方程2-x=|lgx|的两个根为x1，x2，则（ ）
| A．x1x2＜0 | B．x1x2=1 | C．x1x2＞1 | D．0＜x1x2＜1 |
画出函数y=2-x和y=|lgx|的图象，
结合图象易知这两个函数的图象有2交点．
交点的横坐标即为方程2-x=|lgx|的两个根为x1，x2，
结合图形可得：0＜x1＜1，x2＞1，
根据 y=2-x 是减函数，可得 2-x1＜2-x2，即|lgx1|＞|lgx2|，
∴-lgx1＞lgx2，
∴
＞x2，
∴0＜x1x2＜1，
故选D．
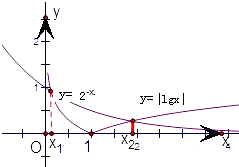
结合图象易知这两个函数的图象有2交点．
交点的横坐标即为方程2-x=|lgx|的两个根为x1，x2，
结合图形可得：0＜x1＜1，x2＞1，
根据 y=2-x 是减函数，可得 2-x1＜2-x2，即|lgx1|＞|lgx2|，
∴-lgx1＞lgx2，
∴
| 1 |
| x1 |
∴0＜x1x2＜1，
故选D．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
有两个不相等的实根，且必有一个根属于
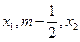成等差数例，设函数
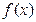的图象的对称轴为
。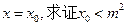