题目内容
设函数f(x)=
,g(x)=ax2+bx(a,b∈R,a≠0)若y=f(x)的图象与y=g(x)图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是( )
| 1 |
| x |
| A.当a<0时,x1+x2<0,y1+y2>0 |
| B.当a<0时,x1+x2>0,y1+y2<0 |
| C.当a>0时,x1+x2<0,y1+y2<0 |
| D.当a>0时,x1+x2>0,y1+y2>0 |
当a<0时,作出两个函数的图象,如图,
因为函数f(x)=
是奇函数,所以A与A′关于原点对称,
显然x2>-x1>0,即x1+x2>0,
-y1>y2,即y1+y2<0
故选B.
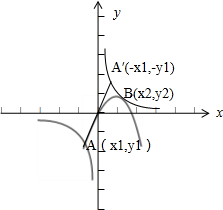
因为函数f(x)=
| 1 |
| x |
显然x2>-x1>0,即x1+x2>0,
-y1>y2,即y1+y2<0
故选B.
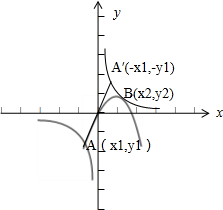

练习册系列答案
相关题目
 是以
是以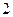 为周期的偶函数,当
为周期的偶函数,当 时,
时,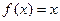 ,那么在区间
,那么在区间 内,关于
内,关于 的方程
的方程 (
( 且
且 )有
)有 个不同的根,则
个不同的根,则 的取值范围是( )
的取值范围是( )




 的方程
的方程 .有一正一负两实数根,则实数
.有一正一负两实数根,则实数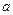 的取值范围________________。
的取值范围________________。