题目内容
已知f(x)是以2为周期的偶函数,当x∈[0,1],f(x)=x,那么在区间[-1,3]内,关于x的方程4f(x)=x+m(其中m为实常数)有四个不同的实根,则m的取值范围是______.
因为关于x的方程4f(x)=x+m有4个不同的根,
就是函数y=f(x)的图象与y=
(x+m)的图象有4个不同的交点,
f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)=x,
所以可以得到函数f(x)的图象
又因为y=
(x+m)是一组斜率为
的平行直线系,
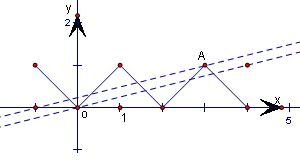
在同一坐标系内画出它们的图象如图,
由图得y=
(x+m)在过点A(3,1)的直线y=
(x+1)和y=
x中间时符合要求,
所以m的取值范围是0<k≤1.
故答案为:(0,1].
就是函数y=f(x)的图象与y=
| 1 |
| 4 |
f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)=x,
所以可以得到函数f(x)的图象
又因为y=
| 1 |
| 4 |
| 1 |
| 4 |
在同一坐标系内画出它们的图象如图,
由图得y=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
所以m的取值范围是0<k≤1.
故答案为:(0,1].


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
