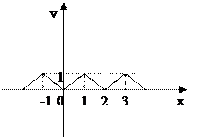题目内容
已知函数f(x)=2(m-1)x2-4mx+2m-1
(1)m为何值时,函数的图象与x轴有两个不同的交点;
(2)如果函数的一个零点在原点,求m的值.
(1)m为何值时,函数的图象与x轴有两个不同的交点;
(2)如果函数的一个零点在原点,求m的值.
(1)函数的图象与x轴有两个不同的交点,有二次项系数 2(m-1)≠0,故m≠1,
且判别式△=16m2-8(m-1)(2m-1)=24m+3>0,故m>
,
综上得:m>
且m≠1.
(2)如果函数的一个零点在原点,则函数图象过原点,f(0)=2m-1=0,
∴m=
.
且判别式△=16m2-8(m-1)(2m-1)=24m+3>0,故m>
| 1 |
| 3 |
综上得:m>
| 1 |
| 3 |
(2)如果函数的一个零点在原点,则函数图象过原点,f(0)=2m-1=0,
∴m=
| 1 |
| 2 |

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 是以
是以 为周期的偶函数,当
为周期的偶函数,当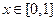 时,
时, ,那么在区间
,那么在区间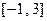 内,关于
内,关于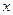 的方程
的方程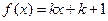 (
( 且
且 )有
)有 个不同的根,则
个不同的根,则 的取值范围是( )
的取值范围是( )