题目内容
9. 如图阴影部分是由曲线y=x2和圆x2+y2=2及x轴围成的封闭图形,则封闭图形的面积S=$\frac{π}{4}-\frac{1}{6}$.
如图阴影部分是由曲线y=x2和圆x2+y2=2及x轴围成的封闭图形,则封闭图形的面积S=$\frac{π}{4}-\frac{1}{6}$.
分析 首先求出曲线的交点,然后求直线y=x与y=x2围成的面积,间接得到所求.
解答 解:曲线y=x2和圆x2+y2=2的在第一象限的交点为(1,1)
所以阴影部分的面积为$\frac{π}{4}$-${∫}_{0}^{1}(x-{x}^{2})dx$=$\frac{π}{4}-(\frac{1}{2}{x}^{2}-\frac{1}{3}{x}^{3}){|}_{0}^{1}$=$\frac{π}{4}-\frac{1}{6}$;
故答案为:$\frac{π}{4}-\frac{1}{6}$.
点评 本题考查了利用定积分求阴影部分的面积,关键是利用定积分表示面积,属于常规题.

练习册系列答案
相关题目
17. 如图,网格纸上小止方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的体积为( )
如图,网格纸上小止方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的体积为( )
 如图,网格纸上小止方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的体积为( )
如图,网格纸上小止方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的体积为( )| A. | 16 | B. | 20 | C. | 4$\sqrt{29}$ | D. | 60 |
4.若某几何体的三视图如图所示,则此几何体的体积是( )
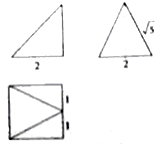

| A. | 4$\sqrt{5}$ | B. | $\frac{4\sqrt{5}}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{4}{3}$ |
1.在直角坐标平面xoy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为$\frac{3}{4}$,则抛物线C的方程为( )
| A. | x2=$\frac{1}{2}$y | B. | x2=y | C. | x2=2y | D. | x2=4y |