题目内容
18.直角三角形ABC中,A为直角,AB=13,AC=3,P、Q为△ABC所在平面内的点,满足$\overrightarrow{AB}$=-2$\overrightarrow{AC}$+3$\overrightarrow{AP}$,$\overrightarrow{CA}$+$\overrightarrow{CB}$=2$\overrightarrow{CQ}$,则$\overrightarrow{AP}$在$\overrightarrow{CQ}$方向上的投影为$\frac{133\sqrt{205}}{615}$.分析 根据题目条件得出$\overrightarrow{AP}$=$\frac{1}{3}$($\overrightarrow{AB}$$+2\overrightarrow{AC}$),$\overrightarrow{CQ}$=$\frac{1}{2}$($\overrightarrow{CA}$+$\overrightarrow{CB}$),利用$\frac{\overrightarrow{AP}•\overrightarrow{CQ}}{|\overrightarrow{CQ}|}$即可求解射影,关键是求解
|$\overrightarrow{CQ}$|,$\overrightarrow{AP}$•$\overrightarrow{CQ}$即可.
解答 解:∵$\overrightarrow{AB}$=-2$\overrightarrow{AC}$+3$\overrightarrow{AP}$,$\overrightarrow{CA}$+$\overrightarrow{CB}$=2$\overrightarrow{CQ}$,
∴$\overrightarrow{AP}$=$\frac{1}{3}$($\overrightarrow{AB}$$+2\overrightarrow{AC}$),
$\overrightarrow{CQ}$=$\frac{1}{2}$($\overrightarrow{CA}$+$\overrightarrow{CB}$),
∵直角三角形ABC中,A为直角,AB=13,AC=3,
∴|$\overrightarrow{CQ}$|=$\sqrt{{\overrightarrow{CQ}}^{2}}$=$\sqrt{\frac{1}{4}({\overrightarrow{AC}}^{2}+2\overrightarrow{CA}•\overrightarrow{CB}+{\overrightarrow{CB}}^{2})}$=$\frac{\sqrt{205}}{2}$,
$\overrightarrow{AP}$•$\overrightarrow{CQ}$=$\frac{1}{6}$($\overrightarrow{AB}$$+2\overrightarrow{AC}$)•($\overrightarrow{AB}$$-2\overrightarrow{AC}$)=$\frac{1}{6}$(169-4×9)=$\frac{133}{6}$,
∴$\frac{\overrightarrow{AP}•\overrightarrow{CQ}}{|\overrightarrow{CQ}|}$=$\frac{\frac{133}{6}}{\frac{\sqrt{205}}{2}}$=$\frac{133\sqrt{205}}{615}$
故答案为:$\frac{133\sqrt{205}}{615}$.
点评 本题给出三角形的向量等式,求向量的投影,着重考查了向量的加法法则、向量数量积的运算性质和向量在几何中的应用等知识,属于中档题

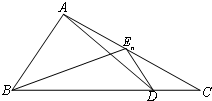 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}=3\overrightarrow{DC}$,En(n∈N+)为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)\overrightarrow{{E_n}D}$,其中实数列{an}中
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}=3\overrightarrow{DC}$,En(n∈N+)为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)\overrightarrow{{E_n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )
| A. | 2•3n-1-1 | B. | 2n-1 | C. | 3n-2 | D. | 3•2n-1-2 |
| A. | -1+i | B. | -1-i | C. | 1-i | D. | 1+i |
 如图阴影部分是由曲线y=x2和圆x2+y2=2及x轴围成的封闭图形,则封闭图形的面积S=$\frac{π}{4}-\frac{1}{6}$.
如图阴影部分是由曲线y=x2和圆x2+y2=2及x轴围成的封闭图形,则封闭图形的面积S=$\frac{π}{4}-\frac{1}{6}$. 定义运算“?”,两个实数a,b的“a?b”运算如图所示,若输入a=2cos$\frac{2015π}{3}$b=2,则输出P的值为( )
定义运算“?”,两个实数a,b的“a?b”运算如图所示,若输入a=2cos$\frac{2015π}{3}$b=2,则输出P的值为( )