题目内容
1.在直角坐标平面xoy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为$\frac{3}{4}$,则抛物线C的方程为( )| A. | x2=$\frac{1}{2}$y | B. | x2=y | C. | x2=2y | D. | x2=4y |
分析 由已知条件推导出点Q到抛物线C的准线的距离为$\frac{p}{4}$+$\frac{p}{2}$=$\frac{3}{4}$,由此能求出抛物线C的方程.
解答 解:抛物线C:x2=2py(p>0)的焦点F(0,$\frac{p}{2}$),
设M(x0,$\frac{{{x}_{0}}^{2}}{2p}$),x0>0,Q(a,b),
由题意知b=$\frac{p}{4}$,
则点Q到抛物线C的准线的距离为b+$\frac{p}{2}$=$\frac{p}{4}$+$\frac{p}{2}$=$\frac{3}{4}$,
解得p=1,
∴抛物线C的方程为x2=2y.
故选:C.
点评 本题考查抛物线的简单性质、直线与抛物线的位置关系,考查数形结合思想,属中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
11.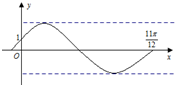 已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分函数图象如图所示,且图象经过点(0,1)和 ($\frac{11π}{12}$,0),则( )
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分函数图象如图所示,且图象经过点(0,1)和 ($\frac{11π}{12}$,0),则( )
 已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分函数图象如图所示,且图象经过点(0,1)和 ($\frac{11π}{12}$,0),则( )
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分函数图象如图所示,且图象经过点(0,1)和 ($\frac{11π}{12}$,0),则( )| A. | ω=$\frac{10}{11}$,φ=$\frac{π}{6}$ | B. | ω=2,φ=$\frac{π}{12}$ | C. | ω=2,φ=$\frac{π}{6}$ | D. | ω=$\frac{10}{11}$,φ=$\frac{π}{12}$ |
16.若复数z=a+bi(i为虚数单位,a,b∈R)在复平面内对应点为Z(a,b),O为坐标原点,将实轴非负半轴绕点O逆时针旋转到OZ,转过的最小角叫复数z的辐角主值,记作arg(z),则arg($\frac{2}{1-i}$)的值为( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{5π}{4}$ | D. | $\frac{7π}{4}$ |
10.计算$\frac{2i}{1-i}$(i为虚数单位)等于( )
| A. | -1+i | B. | -1-i | C. | 1-i | D. | 1+i |
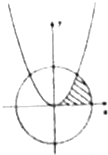 如图阴影部分是由曲线y=x2和圆x2+y2=2及x轴围成的封闭图形,则封闭图形的面积S=$\frac{π}{4}-\frac{1}{6}$.
如图阴影部分是由曲线y=x2和圆x2+y2=2及x轴围成的封闭图形,则封闭图形的面积S=$\frac{π}{4}-\frac{1}{6}$.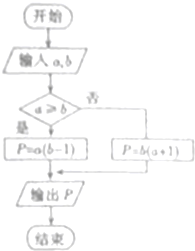 定义运算“?”,两个实数a,b的“a?b”运算如图所示,若输入a=2cos$\frac{2015π}{3}$b=2,则输出P的值为( )
定义运算“?”,两个实数a,b的“a?b”运算如图所示,若输入a=2cos$\frac{2015π}{3}$b=2,则输出P的值为( )