题目内容
14.已知函数f(x)=$\frac{x}{lnx}$-ax(a>0,a≠1)(1)若函数f(x)在[e,e2]上为单调增函数,求实数a的取值范围;
(2)若?x1,x2∈[e,e2],使f(x1)≤f'(x2)+a成立,求实数a的取值范围.
分析 (1)先求导,再分离参数,构造函数,利用导数求出函数的最小值即可;
(2)?x1,x2∈[e,e2],使f(x1)≤f(x2)成立”可化为“当x∈[e,e2]时,有f(x)min≤f'(x)max+a”;而知f′(x)max=$\frac{1}{4}$-a,可化为“当x∈[e,e2]时,有f(x)min≤$\frac{1}{4}$”,分①a≥$\frac{1}{4}$,②a<两种情况讨论:当a<$\frac{1}{4}$时易求f(x)min,当a<$\frac{1}{4}$时可求得f′(x)的值域为[-a,$\frac{1}{4}$-a],再按(i)-a≥0,(ii)-a<0两种情况讨论即可
解答 解:(1)∵f(x)在[e,e2]上为单调增函数,
∴f′(x)=$\frac{lnx-1}{l{n}^{2}x}$-a≥0在[e,e2]恒成立,
∴a≤$\frac{lnx-1}{l{n}^{2}x}$在[e,e2]恒成立,
令g(x)=$\frac{lnx-1}{l{n}^{2}x}$,
则g′(x)=$\frac{lnx(2-lnx)}{xl{n}^{4}x}$,
令g′(x)≤0,即x∈[1,e2],
∴g(x)在[e,e2]上为单调减函数,
∴g(x)min=g(e2)=$\frac{1}{4}$,
∴a≤$\frac{1}{4}$;
故a的取值范围为(0,$\frac{1}{4}$].
(2)“若?x1,x2∈[e,e2],使f(x1)≤f'(x2)+a成立”等价于“当x∈[e,e2]时,有f(x)min≤f′(x)max+a”,
由(1),当x∈[e,e2]时,f′(x)max=$\frac{1}{4}$-a,
∴f′(x)max+a=$\frac{1}{4}$,
问题等价于:“当x∈[e,e2]时,有f(x)min≤$\frac{1}{4}$”,
①当a≥$\frac{1}{4}$时,由(1)知,f(x)在[e,e2]上为减函数,
则f(x)min=f(e2)=$\frac{{e}^{2}}{2}$-ae2≤$\frac{1}{4}$,故a≥$\frac{1}{2}$-$\frac{1}{4{e}^{2}}$;
②当a<$\frac{1}{4}$时,由于f′(x)在[e,e2]上为增函数,
故f′(x)的值域为[f′(e),f′(e2)],即f′(x)的值域为[-a,$\frac{1}{4}$-a],
(i)若-a≥0,即a≤0,f′(x)≥0在[e,e2]上恒成立,故f(x)在[e,e2]上为增函数,
于是,f(x)min=f(e)=e-ae≥e>$\frac{1}{4}$,不合题意;
(ii)(ii)若-a<0,即0<a<$\frac{1}{4}$,
由f′(x)的单调性和值域知,
?唯一x0∈(e,e2),使f′(x0)=0,且满足:
当x∈(e,x0)时,f′(x)<0,f(x)为减函数;
当x∈(x0,e2)时,f′(x)>0,f(x)为增函数;
∴f(x)min=f(x0)=$\frac{{x}_{0}}{ln{x}_{0}}$-ax0≤$\frac{1}{4}$;x0∈(e,e2),
∴a≥$\frac{1}{ln{x}_{0}}$-$\frac{1}{4{x}_{0}}$>$\frac{1}{ln{e}^{2}}$-$\frac{1}{4e}$>$\frac{1}{2}$$-\frac{1}{4}$=$\frac{1}{4}$,
与0<a<$\frac{1}{4}$矛盾,不合题意.
综上,a≥$\frac{1}{2}$-$\frac{1}{4{e}^{2}}$.
点评 本题考查利用导数研究函数的单调性、闭区间上函数的最值,考查恒成立问题,考查分类讨论思想、转化思想,考查学生分析解决问题的能力,属于难题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | [1,2] | B. | [1,2) | C. | [1,2) | D. | (1,2] |
| A. | $\frac{3}{8}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{8}$ | D. | $\frac{1}{3}$ |
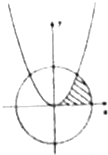 如图阴影部分是由曲线y=x2和圆x2+y2=2及x轴围成的封闭图形,则封闭图形的面积S=$\frac{π}{4}-\frac{1}{6}$.
如图阴影部分是由曲线y=x2和圆x2+y2=2及x轴围成的封闭图形,则封闭图形的面积S=$\frac{π}{4}-\frac{1}{6}$.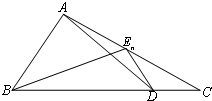 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}=3\overrightarrow{DC}$,En(n∈N+)为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)\overrightarrow{{E_n}D}$,其中实数列{an}中
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}=3\overrightarrow{DC}$,En(n∈N+)为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)\overrightarrow{{E_n}D}$,其中实数列{an}中