题目内容
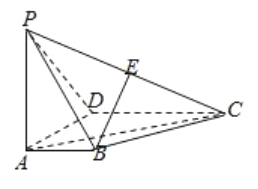
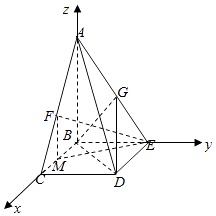
【题目】如图所示,在四棱锥A﹣BCDE中,AB⊥平面BCDE,四边形BCDE为矩形,F为AC的中点,AB=BC=2,BE= ![]() .
.
(Ⅰ)证明:EF⊥BD;
(Ⅱ)在线段AE上是否存在一点G,使得二面角D﹣BG﹣E的大小为 ![]() ?若存在,求
?若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】证明:(Ⅰ)取BC的中点M,连接MF,ME,
∵AB⊥平面BCDE,MF∥AB,
∴MF⊥平面BCDE,又BD平面BCDE,∴MF⊥BD.
在Rt△MBE与Rt△BED中,
∵ ![]() =
= ![]() =
= ![]() ,∴Rt△MBE∽Rt△BED.
,∴Rt△MBE∽Rt△BED.
∴∠BME=∠EBD,而∠BME+∠BEM=90°,
于是∠BEM+∠EBD=90°,∴ME⊥BD,
又∵MF∩ME=M,∴BD⊥平面MEF,
又∵EF平面MEF,∴EF⊥BD.
解:(Ⅱ)∵AB⊥平面BCDE,四边形BCDE为矩形,
∴以B为原点,分别以 ![]() 、
、 ![]() 、
、 ![]() 的方向为x轴、y轴、z轴的正方向建立空间直角坐标系,
的方向为x轴、y轴、z轴的正方向建立空间直角坐标系,
设AG=λAE,依题意可得B(0,0,0),C(2,0,0),
D(2, ![]() ,0),A(0,0,2),E(0,
,0),A(0,0,2),E(0, ![]() ,0),F(1,0,1),
,0),F(1,0,1),
∴ ![]() =
= ![]() +
+ ![]() =
= ![]() +λ
+λ ![]() =(0,
=(0, ![]() λ,2﹣2λ),
λ,2﹣2λ), ![]() =(2,
=(2, ![]() ,0),
,0),
设平面BGD的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 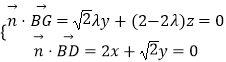 ,取x=1,则
,取x=1,则 ![]() =(1,﹣
=(1,﹣ ![]() ,
, ![]() ),
),
平面BGE的法向量为 ![]() =(1,0,0),
=(1,0,0),
∵二面角D﹣BG﹣E的大小为 ![]() ,
,
∴|cos< ![]() ,
, >|=
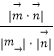 =
= ![]() =
= ![]() ,解得λ=
,解得λ= ![]() .
.
∴存在一点G,且 ![]() =
= ![]() 时,二面角D﹣BG﹣E的大小为
时,二面角D﹣BG﹣E的大小为 ![]() .
.
【解析】(Ⅰ)求两条异面直线互相垂直,可以求得一直线垂直于另一直线所在平面,进而证明两条异面直线互相垂直;(Ⅱ)根据题意建立合适的空间直角坐标系,令二面角D﹣BG﹣E的大小为![]() ,求得此时点G的位置,即可解题 .
,求得此时点G的位置,即可解题 .
【考点精析】利用空间中直线与直线之间的位置关系对题目进行判断即可得到答案,需要熟知相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案