题目内容
【题目】在直角坐标系![]() 中,圆
中,圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求圆![]() 的标准方程;
的标准方程;
(II)设![]() 为圆
为圆![]() 上的两个动点,
上的两个动点, ![]() ,若直线
,若直线![]() 和
和![]() 的斜率之积为定值2,试探求
的斜率之积为定值2,试探求![]() 的最小值.
的最小值.
【答案】(I)见解析(II) 当![]() 时,
时, ![]() 最小值为
最小值为![]() .
.
【解析】试题分析:(1)根据直线和圆的位置关系得到圆心和半径,得到圆的方程;(2)根据题意得到 ,通过换元求得函数的最值即可。
,通过换元求得函数的最值即可。
解析:
(I)因为圆C与y轴相切于点![]() ,所以圆心
,所以圆心![]() 的纵坐标
的纵坐标![]() .
.
因为圆心![]() 在直线
在直线![]() 上,所以
上,所以![]() ,
,
又由圆![]() 与
与![]() 轴相切,可得圆的半径为 2 .
轴相切,可得圆的半径为 2 .
所以![]() 的方程为:
的方程为: ![]() .
.
(II)依题意,知![]() 心不与
心不与![]() 重合,
重合,
故不妨设直线![]() 方程为:
方程为: ![]() .
.
因为圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
因为直线![]() 和
和![]() 的斜率之积为定值-2,
的斜率之积为定值-2,
所以直线![]() 的斜率为:
的斜率为: ![]() ,
,
同![]() 的求解方法,可得
的求解方法,可得 ,
,
所以![]() ,
,
化简得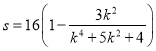 .
.
考察![]() ,
,
令![]() ,得
,得![]() .
.
由![]() 有正数解,且
有正数解,且![]() ,
,
得 ,
,
解得![]() .
.
故 .
.
因为当![]() 时,可解得
时,可解得![]() ,
,
所以当![]() 时,
时, ![]() 最小值为
最小值为![]() .
.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目