题目内容
【题目】如图,在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
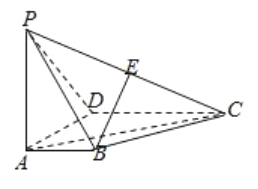
(1)求直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)证明: ![]() .
.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)取PD中点M,连结EM,AM.推导出四边形ABEM为平行四边形,从而BE∥AM,进而∠MAD为异面直线BE与AD所成角(或补角),由此能求出异面直线BE与AD所成角.
(2)推导出PA⊥CD,CD⊥DA,从而CD⊥平面PAD,进而CD⊥AM,再由BE∥AM,能证明BE⊥CD.
试题解析:
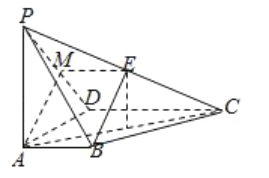
(1)如图,取![]() 中点
中点![]() ,连结
,连结![]() ,
,
由于![]() 分别为
分别为![]() 的中点,故
的中点,故![]() ,
,
又![]() ,
, ![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
∴![]() 为异面直线
为异面直线![]() 与
与![]() 所成角(或补角),
所成角(或补角),
在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,
,
∴异面直线![]() 与
与![]() 所成角为
所成角为![]() .
.
(2)证明:∵![]() 底面
底面![]() ,故
,故![]() ,
,
而![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
又由(1)得![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】已知{an}是公差不为零的等差数列,a1=1,且a1 , a3 , a9成等比数列.
(1)求数列{an}的通项;
(2)设数列{an}的前n项和为Sn , 令 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
