题目内容
设集合W是满足下列两个条件的无穷数列{an}的集合:①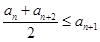 , ②
, ②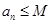 .其中
.其中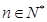 ,
,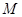 是与
是与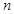 无关的常数.
无关的常数.
(Ⅰ)若{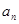 }是等差数列,
}是等差数列,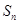 是其前
是其前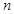 项的和,
项的和,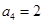 ,
,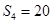 ,证明:
,证明: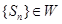 ;
;
(Ⅱ)设数列{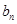 }的通项为
}的通项为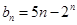 ,且
,且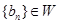 ,求
,求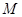 的取值范围;
的取值范围;
(Ⅲ)设数列{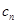 }的各项均为正整数,且
}的各项均为正整数,且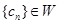 .证明
.证明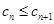 .
.
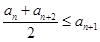 , ②
, ②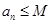 .其中
.其中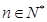 ,
,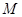 是与
是与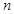 无关的常数.
无关的常数.(Ⅰ)若{
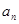 }是等差数列,
}是等差数列,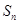 是其前
是其前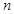 项的和,
项的和,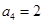 ,
,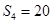 ,证明:
,证明: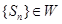 ;
;(Ⅱ)设数列{
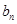 }的通项为
}的通项为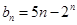 ,且
,且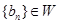 ,求
,求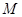 的取值范围;
的取值范围;(Ⅲ)设数列{
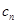 }的各项均为正整数,且
}的各项均为正整数,且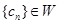 .证明
.证明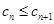 .
.(Ⅰ)见解析(Ⅱ)M≥7(Ⅲ)见解析
解:(Ⅰ)设等差数列{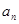 }的公差是d,则
}的公差是d,则 ,解得
,解得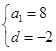 ,
,
所以 (2分)
(2分)
由 =-1<0
=-1<0
得 适合条件①;
适合条件①;
又 所以当n=4或5时,
所以当n=4或5时,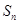 取得最大值20,即
取得最大值20,即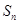 ≤20,适合条件②
≤20,适合条件②
综上,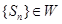 (4分)
(4分)
(Ⅱ)因为 ,所以当n≥3时,
,所以当n≥3时, ,此时数列{bn}单调递减;当n=1,2时,
,此时数列{bn}单调递减;当n=1,2时, ,即b1<b2<b3,因此数列{bn}中的最大项是b3=7
,即b1<b2<b3,因此数列{bn}中的最大项是b3=7
所以M≥7 (8分)
(Ⅲ) 假设存在正整数k,使得 成立
成立
由数列{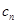 }的各项均为正整数,可得
}的各项均为正整数,可得 ,即
,即
因为 ,所以
,所以
由
因为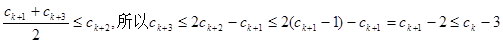
……………………依次类推,可得
设
这显然与数列{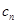 }的各项均为正整数矛盾!
}的各项均为正整数矛盾!
所以假设不成立,即对于任意n∈N*,都有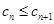 成立. ( 14分)
成立. ( 14分)
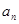 }的公差是d,则
}的公差是d,则 ,解得
,解得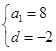 ,
,所以
 (2分)
(2分)由
 =-1<0
=-1<0得
 适合条件①;
适合条件①;又
 所以当n=4或5时,
所以当n=4或5时,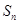 取得最大值20,即
取得最大值20,即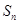 ≤20,适合条件②
≤20,适合条件②综上,
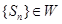 (4分)
(4分)(Ⅱ)因为
 ,所以当n≥3时,
,所以当n≥3时, ,此时数列{bn}单调递减;当n=1,2时,
,此时数列{bn}单调递减;当n=1,2时, ,即b1<b2<b3,因此数列{bn}中的最大项是b3=7
,即b1<b2<b3,因此数列{bn}中的最大项是b3=7所以M≥7 (8分)
(Ⅲ) 假设存在正整数k,使得
 成立
成立由数列{
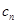 }的各项均为正整数,可得
}的各项均为正整数,可得 ,即
,即
因为
 ,所以
,所以
由

因为
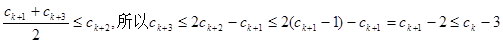
……………………依次类推,可得

设

这显然与数列{
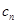 }的各项均为正整数矛盾!
}的各项均为正整数矛盾!所以假设不成立,即对于任意n∈N*,都有
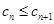 成立. ( 14分)
成立. ( 14分) 
练习册系列答案
相关题目
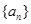 为等差数列,
为等差数列,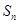 为其前
为其前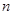 项和,若
项和,若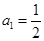 ,
,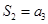 ,则
,则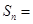 ___________.
___________.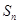 为等差数列
为等差数列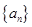 的前
的前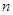 项和,若
项和,若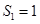 ,
,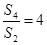 ,则
,则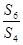 的值为( )
的值为( )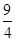
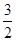
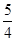
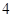
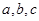 是三个连续的自然数,且成等差数列,
是三个连续的自然数,且成等差数列,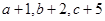 成等比数列,求
成等比数列,求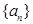 中
中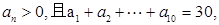 则
则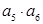 的最大值等于
的最大值等于 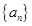 中,
中,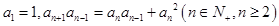 ,
,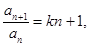
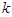
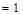 ;(2)求数列
;(2)求数列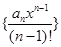 的前
的前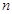 项和。
项和。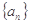 的前
的前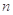 项和
项和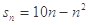 ,
,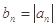 求 数列
求 数列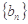 的前
的前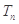 。
。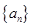 的前n项和为
的前n项和为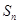 ,若
,若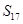 为一确定常数,则下列各式也为确定常数的是( )
为一确定常数,则下列各式也为确定常数的是( )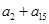
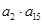
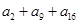
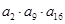
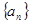 中,
中, 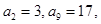 求
求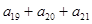 的值。
的值。