题目内容
(本小题满分12分)已知数列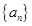 中,
中,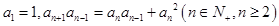 ,
,
且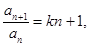
(1)求证: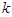
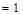 ;(2)求数列
;(2)求数列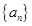 的通项公式;(3)求数列
的通项公式;(3)求数列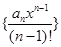 的前
的前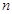 项和。
项和。
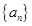 中,
中,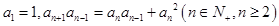 ,
,且
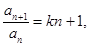
(1)求证:
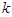
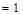 ;(2)求数列
;(2)求数列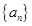 的通项公式;(3)求数列
的通项公式;(3)求数列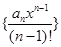 的前
的前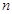 项和。
项和。(1) .
.
(2)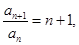
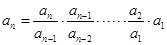 =
=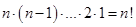
(3)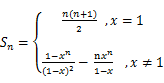
 .
. (2)
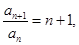
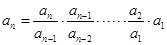 =
=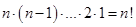
(3)
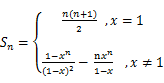
本试题主要是考查了数列的递推关系的运用。求解通项公式和数列的和的综合运用。
(1)根据已知递推关系,对n令值,得到前两项的关系式,然后结合项之间的关系得到参数k的值。
(2)在地怀疑问的基础上,分析通项公式的特点,然后运用错位相减法求解和,得到结论。
解:
(1) , 故
, 故 ,
,
又因为
则
 ,即
,即 .
.
所以 .
.
(3)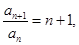
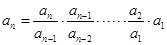 =
=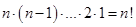
(4) 因为 设其前n项和为
设其前n项和为  ,
,
所以,当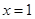 时,
时,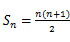 ,
,
当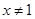 时,
时, ……… (1)
……… (1)
 得
得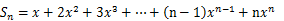 ……(2)
……(2)
由(1)-(2)得:

综上所述: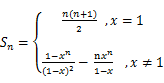
(1)根据已知递推关系,对n令值,得到前两项的关系式,然后结合项之间的关系得到参数k的值。
(2)在地怀疑问的基础上,分析通项公式的特点,然后运用错位相减法求解和,得到结论。
解:
(1)
 , 故
, 故 ,
,又因为

则

 ,即
,即 .
.所以
 .
. (3)
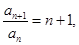
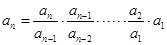 =
=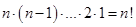
(4) 因为
 设其前n项和为
设其前n项和为  ,
, 所以,当
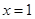 时,
时,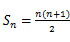 ,
, 当
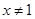 时,
时, ……… (1)
……… (1) 得
得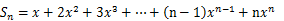 ……(2)
……(2)由(1)-(2)得:


综上所述:
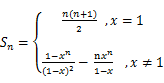

练习册系列答案
相关题目
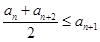 , ②
, ②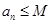 .其中
.其中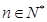 ,
,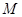 是与
是与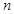 无关的常数.
无关的常数.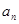 }是等差数列,
}是等差数列,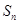 是其前
是其前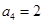 ,
,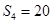 ,证明:
,证明: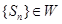 ;
;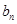 }的通项为
}的通项为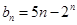 ,且
,且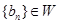 ,求
,求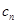 }的各项均为正整数,且
}的各项均为正整数,且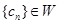 .证明
.证明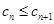 .
.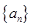 中,
中,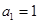 ,
,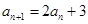 ,
,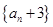 是等比数列;
是等比数列; 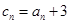 ,
,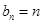 ,求数列
,求数列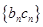 的前
的前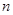 项和
项和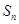 .
. 中,
中, ,
,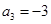 .
.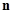 项和
项和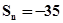 ,求
,求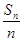 ),Q(n+2,
),Q(n+2, 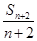 )(n∈N+*)的直线的斜率为( )
)(n∈N+*)的直线的斜率为( )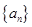 的前
的前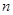 项和为
项和为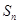 ,若
,若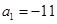 ,
,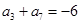 ,则当
,则当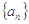 中,
中,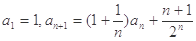
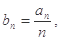 求数列
求数列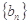 的通项公式
的通项公式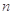 项和
项和 。
。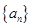 是首项为
是首项为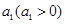 ,公差为
,公差为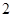 的等差数列,其前
的等差数列,其前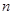 项和为
项和为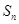 ,且
,且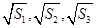 成等差数列.
成等差数列.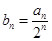 的前
的前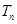 ,求
,求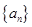 的公比
的公比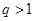 ,
, 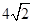 是
是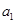 和
和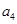 的一个等比中项,
的一个等比中项,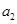 和
和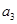 的等差中项为
的等差中项为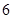 ,若数列
,若数列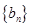 满足
满足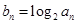 (
(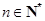 ).
).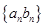 的前
的前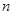 项和
项和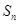 .
.