题目内容
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在[495,510)内的产品为合格品,否则为不合格品.统计结果如下:
甲流水线样本的频数分布表
产品重量(克) | 频数 |
[490,495) | 6 |
[495,500) | 8 |
[500,505) | 14 |
[505,510) | 8 |
[510,515] | 4 |
乙流水线样本的频率分布直方图
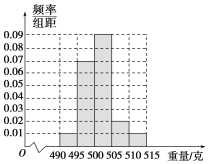
(1)求甲流水线样本合格的频率;
(2)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
分类 | 甲流水线 | 乙流水线 | 总计 |
合格品 | |||
不合格品 | |||
总计 |
附:K2=![]() .
.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(1)![]() ; (2)有
; (2)有![]() 的把握认为产品的包装质量与两条自动包装流水线的选择有关.
的把握认为产品的包装质量与两条自动包装流水线的选择有关.
【解析】
(1)利用频率分布直方图计算样本合格的频率;(2)完善2×2列联表,代入![]() 公式求解.
公式求解.
(1)由表知甲流水线样本中合格品数为8+14+8=30,故甲流水线样本中合格品的频率为![]() =0.75.
=0.75.
(2)由(1)知甲流水线样本中合格品格数30,乙流水线样本中合格品数为0.9×40=36.
则2×2列联表如下:
分类 | 甲流水线 | 乙流水线 | 总计 |
合格品 | 30 | 36 | 66 |
不合格品 | 10 | 4 | 14 |
总计 | 40 | 40 | 80 |
由2×2列联表中的数据得K2的观测值为
K=![]() ≈3.12>2.706.
≈3.12>2.706.
故有90%的把握认为产品的包装质量与两条自动包装流水线的选择有关.

【题目】已知f(x)=ln(mx+1)﹣2(m≠0).
(1)讨论f(x)的单调性;
(2)若m>0,g(x)=f(x)+ ![]() 存在两个极值点x1 , x2 , 且g(x1)+g(x2)<0,求m的取值范围.
存在两个极值点x1 , x2 , 且g(x1)+g(x2)<0,求m的取值范围.
【题目】某公司过去五个月的广告费支出![]() 与销售额
与销售额![]() (单位:万元)之间有下列对应数据:
(单位:万元)之间有下列对应数据:
| 2 | 4 | 5 | 6 | 8 |
|
| 40 | 60 | 50 | 70 |
工作人员不慎将表格中![]() 的第一个数据丢失.已知
的第一个数据丢失.已知![]() 对
对![]() 呈线性相关关系,且回归方程为
呈线性相关关系,且回归方程为![]() ,则下列说法:①销售额
,则下列说法:①销售额![]() 与广告费支出
与广告费支出![]() 正相关;②丢失的数据(表中
正相关;②丢失的数据(表中![]() 处)为30;③该公司广告费支出每增加1万元,销售额一定增加
处)为30;③该公司广告费支出每增加1万元,销售额一定增加![]() 万元;④若该公司下月广告投入8万元,则销售
万元;④若该公司下月广告投入8万元,则销售
额为70万元.其中,正确说法有( )
A.1个 B.2个 C.3个 D.4个




