题目内容
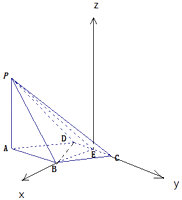
【题目】四棱锥P﹣ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD中点,PA⊥底面ABCD,PA=2. 
(1)证明:平面PBE⊥平面PAB;
(2)求直线PC与平面PBE所成的角的正弦值.
【答案】
(1)证明:连结BD,
∵四棱锥P﹣ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,
∴BD=BC=DC=1,
∵E是CD中点,∴BE⊥DC,
∵AB∥DC,∴BE⊥AB,
∵PA⊥底面ABCD,BE平面ABCD,
∴BE⊥PA,
∵PA∩AB=A,∴BE⊥平面PAB,
∵BE平面PAB,∴平面PBE⊥平面PAB.
(2)解:以E为原点,EB为x轴,EC为y轴,以过点E且垂直于平面ABCD的直线为z轴,
建立空间直角坐标系,
则P( ![]() ,﹣1,2),C(0,
,﹣1,2),C(0, ![]() ,0),B(
,0),B( ![]() ,0,0),E(0,0,0),
,0,0),E(0,0,0),
![]() =(﹣
=(﹣ ![]() ,
, ![]() ,﹣2),
,﹣2), ![]() =(
=( ![]() ,0,0),
,0,0), ![]() =(
=( ![]() ,﹣1,2),
,﹣1,2),
设平面PBE的法向量 ![]() =(x,y,z),
=(x,y,z),
则 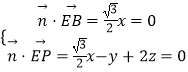 ,取z=1,得
,取z=1,得 ![]() =(0,2,1),
=(0,2,1),
设直线PC与平面PBE所成的角为θ,
则sinθ= 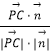 =
= ![]() =
= ![]() .
.
∴直线PC与平面PBE所成的角的正弦值为 ![]() .
.
【解析】(1)连结BD,推导出BE⊥AB,BE⊥PA,从而BE⊥平面PAB,由此能证明平面PBE⊥平面PAB.(2)以E为原点,EB为x轴,EC为y轴,以过点E且垂直于平面ABCD的直线为z轴,建立空间直角坐标系,利用向量法能求出直线PC与平面PBE所成的角的正弦值.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直,以及对空间角的异面直线所成的角的理解,了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则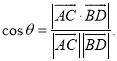 .
.

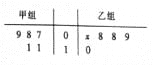
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在[495,510)内的产品为合格品,否则为不合格品.统计结果如下:
甲流水线样本的频数分布表
产品重量(克) | 频数 |
[490,495) | 6 |
[495,500) | 8 |
[500,505) | 14 |
[505,510) | 8 |
[510,515] | 4 |
乙流水线样本的频率分布直方图
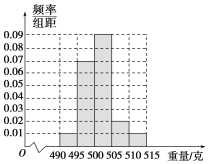
(1)求甲流水线样本合格的频率;
(2)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
分类 | 甲流水线 | 乙流水线 | 总计 |
合格品 | |||
不合格品 | |||
总计 |
附:K2=![]() .
.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |