题目内容
【题目】如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=![]() AD,E,F分别为线段AD,PC的中点.
AD,E,F分别为线段AD,PC的中点.

(1)求证:AP∥平面BEF;
(2)求证:BE⊥平面PAC.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:
(1)证明四边形![]() 是平行四边形,可得
是平行四边形,可得![]() 是
是![]() 的中点,利用
的中点,利用![]() 为线段
为线段![]() 的中点,可得
的中点,可得![]() ,从而可证
,从而可证![]() 平面
平面![]() ;
;
(2)证明![]() ,即可证明
,即可证明![]() 平面
平面![]() .
.
试题解析:
(1)设AC∩BE=O,连接OF,EC.

由于E为AD的中点,
AB=BC=![]() AD,AD∥BC,
AD,AD∥BC,
∴AE∥BC,AE=AB=BC,
因此四边形ABCE为菱形,
∴O为AC的中点.
又F为PC的中点,因此在△PAC中,可得AP∥OF.
又OF平面BEF,AP平面BEF.
∴AP∥平面BEF.
(2)由题意知ED∥BC,ED=BC.
∴四边形BCDE为平行四边形,
因此BE∥CD.
又AP⊥平面PCD,
∴AP⊥CD,
因此AP⊥BE.
∵四边形ABCE为菱形,
∴BE⊥AC.
又AP∩AC=A,AP,AC平面PAC,
∴BE⊥平面PAC.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案【题目】某校高一年级3个班有10名学生在全国英语能力大赛中获奖,学生来源人数如表:
班别 | 高一(1)班 | 高一(2)班 | 高一(3)班 |
人数 | 3 | 6 | 1 |
若要求从10位同学中选出两位同学介绍学习经验,设其中来自高一(1)班的人数为ξ,求随机变量ξ的分布列及数学期望E(ξ).
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在[495,510)内的产品为合格品,否则为不合格品.统计结果如下:
甲流水线样本的频数分布表
产品重量(克) | 频数 |
[490,495) | 6 |
[495,500) | 8 |
[500,505) | 14 |
[505,510) | 8 |
[510,515] | 4 |
乙流水线样本的频率分布直方图
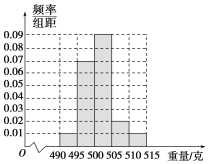
(1)求甲流水线样本合格的频率;
(2)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
分类 | 甲流水线 | 乙流水线 | 总计 |
合格品 | |||
不合格品 | |||
总计 |
附:K2=![]() .
.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |


