题目内容
【题目】《几何原本》卷2的几何代数法（以几何方法研究代数问题）成了后世西方数学家处理问题的重要依据，通过这一原理，很多的代数的公理或定理都能够通过图形实现证明，也称之为无字证明．现有如图所示图形，点F在半圆O上，点C在直径AB上，且OF⊥AB，设AC=a，BC=b，则该图形可以完成的无字证明为（ ） 
A.
（a＞0，b＞0）
B.a2+b2≥2ab（a＞0，b＞0）
C.
（a＞0，b＞0）
D.
（a＞0，b＞0）
【答案】D
【解析】解：由图形可知：OF= 
= 
，OC= 
． 在Rt△OCF中，由勾股定理可得：
CF= 
= 
．
∵CF≥OC，
∴ ≤ ．（a，b＞0）．
故选：D．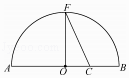
【考点精析】通过灵活运用基本不等式，掌握基本不等式：
,（当且仅当
时取到等号）；变形公式：
即可以解答此题．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况，随机在这两条流水线上各抽取40件产品作为样本，并称出它们的重量(单位：克)，重量值落在[495，510)内的产品为合格品，否则为不合格品．统计结果如下：
甲流水线样本的频数分布表
产品重量(克) | 频数 |
[490，495) | 6 |
[495，500) | 8 |
[500，505) | 14 |
[505，510) | 8 |
[510，515] | 4 |
乙流水线样本的频率分布直方图
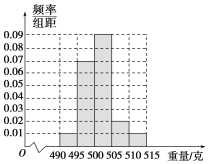
(1)求甲流水线样本合格的频率；
(2)由以上统计数据完成下面2×2列联表，并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关．
分类 | 甲流水线 | 乙流水线 | 总计 |
合格品 | |||
不合格品 | |||
总计 |
附：K2＝
.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
