题目内容
【题目】已知f(x)=ln(mx+1)﹣2(m≠0).
(1)讨论f(x)的单调性;
(2)若m>0,g(x)=f(x)+ ![]() 存在两个极值点x1 , x2 , 且g(x1)+g(x2)<0,求m的取值范围.
存在两个极值点x1 , x2 , 且g(x1)+g(x2)<0,求m的取值范围.
【答案】
(1)解:由已知得mx+1>0,f′(x)= ![]() ,
,
①若m>0时,由mx+1>0,得:x>﹣ ![]() ,恒有f′(x)>0,
,恒有f′(x)>0,
∴f(x)在(﹣ ![]() ,+∞)递增;
,+∞)递增;
②若m<0,由mx+1>0,得:x<﹣ ![]() ,恒有f′(x)<0,
,恒有f′(x)<0,
∴f(x)在(﹣∞,﹣ ![]() )递减;
)递减;
综上,m>0时,f(x)在(﹣ ![]() ,+∞)递增,
,+∞)递增,
m<0时,f(x)在(﹣∞,﹣ ![]() )递减
)递减
(2)解:g(x)=ln(mx+1)+ ![]() ﹣2,(m>0),
﹣2,(m>0),
∴g′(x)= ![]() ,
,
令h(x)=mx2+4m﹣4,
m≥1时,h(x)≥0,g′(x)≥0,g(x)无极值点,
0<m<1时,令h(x)=0,得:x1=﹣2 ![]() 或x2=2
或x2=2 ![]() ,
,
由g(x)的定义域可知x>﹣ ![]() 且x≠﹣2,
且x≠﹣2,
∴﹣2 ![]() >﹣
>﹣ ![]() 且﹣2
且﹣2 ![]() ≠﹣2,解得:m≠
≠﹣2,解得:m≠ ![]() ,
,
∴x1,x2为g(x)的两个极值点,
即x1=﹣2 ![]() ,x2=2
,x2=2 ![]() ,
,
且x1+x2=0,x1x2= ![]() ,得:
,得:
g(x1)+g(x2)=ln(mx1+1)+ ![]() ﹣2+ln(mx2+1)+
﹣2+ln(mx2+1)+ ![]() ﹣2
﹣2
=ln(2m﹣1)2+ ![]() ﹣2,
﹣2,
令t=2m﹣1,F(t)=lnt2+ ![]() ﹣2,
﹣2,
![]() 时,﹣1<t<0,
时,﹣1<t<0,
∴F(t)=2ln(﹣t)+ ![]() ﹣2,
﹣2,
∴F′(t)= ![]() <0,
<0,
∴F(t)在(﹣1,0)递减,F(t)<F(﹣1)<0,
即0<m< ![]() 时,g(x1)+g(x2)<0成立,符合题意;
时,g(x1)+g(x2)<0成立,符合题意;
② ![]() <m<1时,0<t<1,
<m<1时,0<t<1,
∴F(t)=2lnt+ ![]() ﹣2,F′(t)=
﹣2,F′(t)= ![]() <0,
<0,
∴F(t)在(0,1)递减,F(t)>F(1)=0,
∴ ![]() <m<1时,g(x1)+g(x2)>0,不合题意,
<m<1时,g(x1)+g(x2)>0,不合题意,
综上,m∈(0, ![]() )
)
【解析】(1)求出函数的导数,通过讨论m的范围,确定函数的单调性;(2)求出g(x)的导数,通过讨论m的范围,求出函数的单调区间,从而求出函数的最值,判断是否符合题意,从而判断出m的范围即可.
【考点精析】掌握利用导数研究函数的单调性和函数的极值与导数是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案【题目】某校高一年级3个班有10名学生在全国英语能力大赛中获奖,学生来源人数如表:
班别 | 高一(1)班 | 高一(2)班 | 高一(3)班 |
人数 | 3 | 6 | 1 |
若要求从10位同学中选出两位同学介绍学习经验,设其中来自高一(1)班的人数为ξ,求随机变量ξ的分布列及数学期望E(ξ).
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在[495,510)内的产品为合格品,否则为不合格品.统计结果如下:
甲流水线样本的频数分布表
产品重量(克) | 频数 |
[490,495) | 6 |
[495,500) | 8 |
[500,505) | 14 |
[505,510) | 8 |
[510,515] | 4 |
乙流水线样本的频率分布直方图
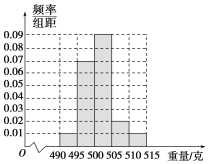
(1)求甲流水线样本合格的频率;
(2)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
分类 | 甲流水线 | 乙流水线 | 总计 |
合格品 | |||
不合格品 | |||
总计 |
附:K2=![]() .
.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |


