题目内容
【题目】极坐标系中椭圆C的方程为ρ2= ![]() ,以极点为原点,极轴为x轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
,以极点为原点,极轴为x轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
(1)若椭圆上任一点坐标为P(x,y),求 ![]() 的取值范围;
的取值范围;
(2)若椭圆的两条弦AB,CD交于点Q,且直线AB与CD的倾斜角互补,求证:|QA||QB|=|QC||QD|.
【答案】
(1)解:∵椭圆C的方程为ρ2= ![]() ,
,
∴椭圆C的直角坐标方程为 ![]() ,
,
设 ![]() ,
,
则 ![]()
= ![]() .
.
∴ ![]() 的取值范围是[1﹣
的取值范围是[1﹣ ![]() ]
]
(2)证明:设直线AB的倾斜角为α,直线CD的倾斜角为π﹣α,Q(x0,y0),
则直线AB的参数方程为 ![]() ,(t为参数),
,(t为参数),
代入x2+2y2=2,得:(x0+tcosα)2+2(y0+tsinα)2﹣2=0,
即(cos2α+2sin2α)t2+(2x0cosα+4y0sinα)t+( ![]() ﹣2)=0,
﹣2)=0,
设A、B对应的参数分别为t1,t2,
则|QA||QB|=|t1t2|=| ![]() |,
|,
同理,|QC||QB|=| ![]() |=|
|=| ![]() |,
|,
∴|QA||QB|=|QC||QD|
【解析】(1)由椭圆C的极坐标方程能椭圆C的直角坐标方程,设 ![]() ,由三角函数性质能求出
,由三角函数性质能求出 ![]() 的取值范围.(2)设直线AB的倾斜角为α,直线CD的倾斜角为π﹣α,Q(x0 , y0),直线AB的参数方程为
的取值范围.(2)设直线AB的倾斜角为α,直线CD的倾斜角为π﹣α,Q(x0 , y0),直线AB的参数方程为 ![]() ,(t为参数),代入x2+2y2=2,得:(x0+tcosα)2+2(y0+tsinα)2﹣2=0,推导出|QA||QB|=|t1t2|=|
,(t为参数),代入x2+2y2=2,得:(x0+tcosα)2+2(y0+tsinα)2﹣2=0,推导出|QA||QB|=|t1t2|=| ![]() |,同理,|QC||QB|=|
|,同理,|QC||QB|=| ![]() |=|
|=| ![]() |,由此能证明|QA||QB|=|QC||QD|.
|,由此能证明|QA||QB|=|QC||QD|.

【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在[495,510)内的产品为合格品,否则为不合格品.统计结果如下:
甲流水线样本的频数分布表
产品重量(克) | 频数 |
[490,495) | 6 |
[495,500) | 8 |
[500,505) | 14 |
[505,510) | 8 |
[510,515] | 4 |
乙流水线样本的频率分布直方图
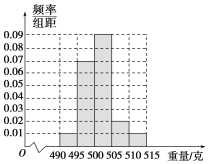
(1)求甲流水线样本合格的频率;
(2)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
分类 | 甲流水线 | 乙流水线 | 总计 |
合格品 | |||
不合格品 | |||
总计 |
附:K2=![]() .
.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |