题目内容
本题14分,第(1)小题6分,第(2)小题8分)
已知函数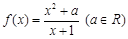 .
.
(1)用定义证明:当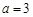 时,函数
时,函数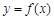 在
在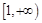 上是增函数;
上是增函数;
(2)若函数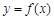 在
在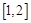 上有最小值
上有最小值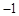 ,求实数
,求实数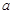 的值.
的值.
已知函数
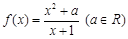 .
. (1)用定义证明:当
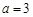 时,函数
时,函数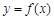 在
在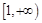 上是增函数;
上是增函数;(2)若函数
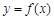 在
在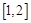 上有最小值
上有最小值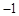 ,求实数
,求实数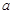 的值.
的值.(1)当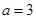 时,
时,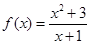
任取 时,
时,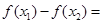
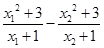
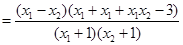
因 为
为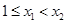 ,所以
,所以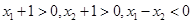
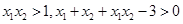
所以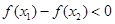 ,所以
,所以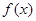 在
在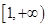 上为增函数。
上为增函数。
(2)解法一、根据题意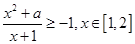 恒成立。且等号成立。
恒成立。且等号成立。
所以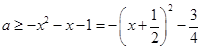
由于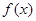 在
在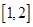 上单调递减,所以
上单调递减,所以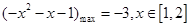
所以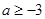 ;
;
当等式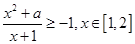 等号成立时,
等号成立时,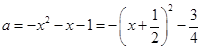
所以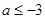 ,
,
故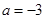
解法二、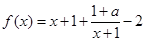 ,令
,令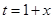 ,则
,则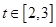
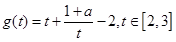
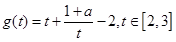
①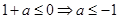 时,根据反比例函数与正比例函数的性质,
时,根据反比例函数与正比例函数的性质,
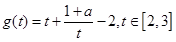 为增函数
为增函数
所以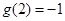 ,即:
,即: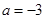
②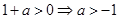 ,由
,由 于
于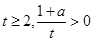 ,所以
,所以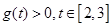 ,即
,即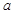 不存在。
不存在。
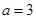 时,
时,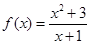
任取
 时,
时,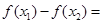
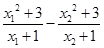
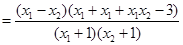
因
 为
为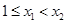 ,所以
,所以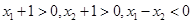
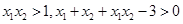
所以
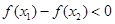 ,所以
,所以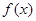 在
在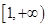 上为增函数。
上为增函数。 (2)解法一、根据题意
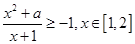 恒成立。且等号成立。
恒成立。且等号成立。 所以
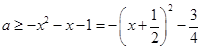
由于
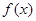 在
在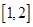 上单调递减,所以
上单调递减,所以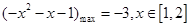
所以
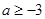 ;
; 当等式
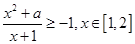 等号成立时,
等号成立时,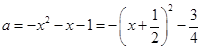
所以
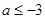 ,
, 故
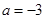
解法二、
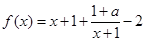 ,令
,令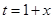 ,则
,则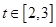
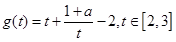
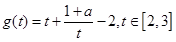
①
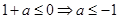 时,根据反比例函数与正比例函数的性质,
时,根据反比例函数与正比例函数的性质,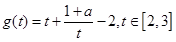 为增函数
为增函数 所以
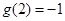 ,即:
,即: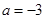
②
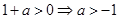 ,由
,由 于
于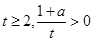 ,所以
,所以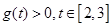 ,即
,即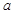 不存在。
不存在。略

练习册系列答案
相关题目
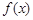 是定义在
是定义在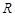 上的奇函数,且当
上的奇函数,且当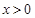 时
时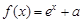 ,若
,若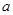 的最小值是
的最小值是 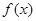 在
在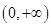 上为增函数,且
上为增函数,且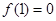 ,则不等式
,则不等式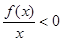 的解集为
的解集为  =0,则不等式f(log4x)>0的解集为 ( )
=0,则不等式f(log4x)>0的解集为 ( )

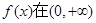 上是增函数,且
上是增函数,且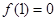 ,则不等式
,则不等式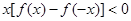 的解集为( )
的解集为( )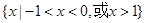

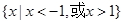
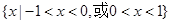
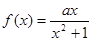
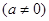 ,
,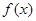 的奇偶性;
的奇偶性;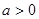 时,判断
时,判断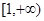 上的单调性并给出证明。
上的单调性并给出证明。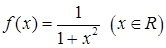 的值域是( )
的值域是( )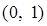
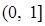
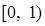
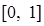
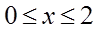 ,求函数
,求函数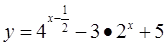 的最大值与最小值。
的最大值与最小值。