题目内容
已知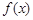 是定义在
是定义在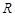 上的奇函数,且当
上的奇函数,且当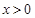 时
时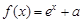 ,若
,若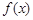 在
在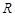 上是单调函数,则实数
上是单调函数,则实数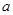 的最小值是
的最小值是
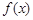 是定义在
是定义在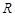 上的奇函数,且当
上的奇函数,且当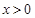 时
时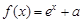 ,若
,若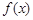 在
在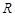 上是单调函数,则实数
上是单调函数,则实数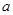 的最小值是
的最小值是 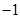
当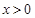 时
时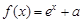 ,且
,且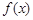 在
在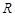 上是单调函数,则f(x)在R上单调递增,又
上是单调函数,则f(x)在R上单调递增,又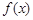 是定义在
是定义在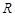 上的奇函数,f(0)=0,因此
上的奇函数,f(0)=0,因此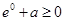 ,即
,即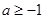 。
。
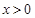 时
时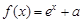 ,且
,且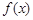 在
在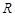 上是单调函数,则f(x)在R上单调递增,又
上是单调函数,则f(x)在R上单调递增,又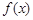 是定义在
是定义在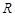 上的奇函数,f(0)=0,因此
上的奇函数,f(0)=0,因此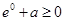 ,即
,即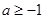 。
。
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
题目内容
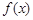 是定义在
是定义在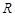 上的奇函数,且当
上的奇函数,且当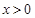 时
时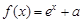 ,若
,若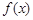 在
在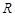 上是单调函数,则实数
上是单调函数,则实数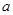 的最小值是
的最小值是 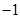
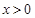 时
时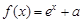 ,且
,且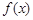 在
在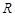 上是单调函数,则f(x)在R上单调递增,又
上是单调函数,则f(x)在R上单调递增,又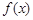 是定义在
是定义在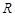 上的奇函数,f(0)=0,因此
上的奇函数,f(0)=0,因此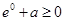 ,即
,即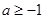 。
。
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案