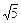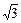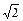题目内容
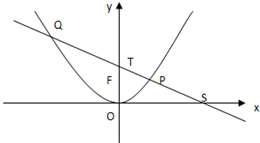
已知抛物线y=-
与过点M(0,-1)的直线l相交于A、B两点,O为原点.若OA和OB的斜率之和为1.
(1)求直线l的方程;
(2)求△AOB的面积.
| x2 |
| 2 |
(1)求直线l的方程;
(2)求△AOB的面积.
(1)显然直线l的斜率必存在,设直线l的方程为y=kx-1,A(x1,y1),B(x2,y2),
由
得x2+2kx-2=0,
∴x1+x2=-2k,x1x2=-2.
∵
+
=1,
∴
+
=2k-
=2k-
=1,解得k=1
所以直线l的方程为y=x-1.
(2)解法1:∵|x1-x2|=
=2
,|OM|=1.
∴S△AOB=
|x1-x2||OM|=
.
解法2:∵|AB|=
|x1-x2|=
=2
.
h=
.
S△AOB=
|AB|•h=
.
由
|
∴x1+x2=-2k,x1x2=-2.
∵
| y1 |
| x1 |
| y2 |
| x2 |
∴
| kx1-1 |
| x1 |
| kx2-1 |
| x2 |
| x1+x2 |
| x1x2 |
| -2k |
| -2 |
所以直线l的方程为y=x-1.
(2)解法1:∵|x1-x2|=
| 4k2+8 |
| 3 |
∴S△AOB=
| 1 |
| 2 |
| 3 |
解法2:∵|AB|=
| 1+K2 |
| 1+K2 |
| 4k2+8 |
| 6 |
h=
| 1 | ||
|
S△AOB=
| 1 |
| 2 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
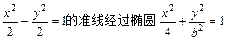 (b>0)的焦点,则b=()
(b>0)的焦点,则b=()