题目内容
如图,椭圆C:x2+3y2=3b2(b>0).
(1)求椭圆C的离心率;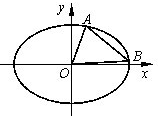
(2)若b=1,A,B是椭圆C上两点,且|AB|=
,求△AOB面积的最大值.
(1)求椭圆C的离心率;

(2)若b=1,A,B是椭圆C上两点,且|AB|=
| 3 |
(1)由x2+3y2=3b2 得
+
=1,
所以e=
=
=
;
(2)设A(x1,y1),B(x2,y2),△ABO的面积为S.
如果AB⊥x轴,由对称性不妨记A的坐标为(
,
),此时S=
•
•
=
;
如果AB不垂直于x轴,设直线AB的方程为y=kx+m,代入椭圆方程,可得x2+3(kx+m) 2=3,
即(1+3k2)x2+6kmx+3m2-3=0,又△=36k2m2-4(1+3k2) (3m2-3)>0,
所以x1+x2=-
,x1x2=
,
所以(x1-x2)2=(x1+x2)2-4x1x2=
,①
由|AB|=
•|x1-x2|及|AB|=
得(x1-x2)2=
,②
结合①,②得m2=(1+3k2)-
.
又原点O到直线AB的距离为
,
所以S=
•
•
,
因此S2=
•
=
(
-2)2+
≤
,
故S≤
,当且仅当
=2,即k=±1时上式取等号.
又
>
,故Smax=
.

| x2 |
| 3b2 |
| y2 |
| b2 |
所以e=
| c |
| a |
| ||
|
| ||
| 3 |
(2)设A(x1,y1),B(x2,y2),△ABO的面积为S.
如果AB⊥x轴,由对称性不妨记A的坐标为(
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 4 |
如果AB不垂直于x轴,设直线AB的方程为y=kx+m,代入椭圆方程,可得x2+3(kx+m) 2=3,
即(1+3k2)x2+6kmx+3m2-3=0,又△=36k2m2-4(1+3k2) (3m2-3)>0,
所以x1+x2=-
| 6km |
| 1+3k2 |
| 3m2-3 |
| 1+3k2 |
所以(x1-x2)2=(x1+x2)2-4x1x2=
| 12(1+3k2-m2) |
| (1+3k2)2 |
由|AB|=
| 1+k2 |
| 3 |
| 3 |
| 1+k2 |
结合①,②得m2=(1+3k2)-
| (1+3k2)2 |
| 4(1+k2) |
又原点O到直线AB的距离为
| |m| | ||
|
所以S=
| 1 |
| 2 |
| |m| | ||
|
| 3 |
因此S2=
| 3 |
| 4 |
| m2 |
| 1+k2 |
| 3 |
| 16 |
| 1+3k2 |
| 1+k2 |
| 3 |
| 4 |
| 3 |
| 4 |
故S≤
| ||
| 2 |
| 1+3k2 |
| 1+k2 |
又
| ||
| 2 |
| 3 |
| 4 |
| ||
| 2 |


练习册系列答案
相关题目
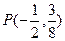 和到直线
和到直线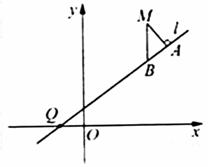
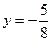 距离相等的点的轨迹,l是过点Q(-1,0)的直线,
距离相等的点的轨迹,l是过点Q(-1,0)的直线,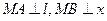
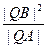 为常数。
为常数。