题目内容
已知椭圆C:
+
=1(a>b>0)的左焦点为F(-1,0),离心率为
,过点F的直线l与椭圆C交于A、B两点.
(Ⅰ)求椭圆C的方程;
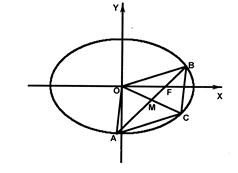
(Ⅱ)设过点F不与坐标轴垂直的直线交椭圆C于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设过点F不与坐标轴垂直的直线交椭圆C于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
(Ⅰ)由题意可知:c=1,a2=b2-c2,e=
=
…(2分)
解得:a=
,b=1(3分)
故椭圆的方程为:
+y2=1(4分)
(II)设直线AB的方程为y=k(x+1)(k≠0),(5分)
联立,得
,
整理得(1+2k2)x2+4k2x+2k2-2=0(7分)
∵直线AB过椭圆的左焦点F∴方程有两个不等实根.(8分)
记A(x1,y1),B(x2,y2),AB的中点N(x0,y0)
则x1+x2=
(9分)
x0=
,y0=
(10分)
垂直平分线NG的方程为y-y0=-
(x-x0),(11分)
令y=0,得xG=x0+ky0=-
+
=-
=-
+
.(12分)
∵k≠0,∴-
<xG<0(13分)
∴点G横坐标的取值范围为(-
,0).(14分)
| c |
| a |
| ||
| 2 |
解得:a=
| 2 |
故椭圆的方程为:
| x2 |
| 2 |
(II)设直线AB的方程为y=k(x+1)(k≠0),(5分)
联立,得
|
整理得(1+2k2)x2+4k2x+2k2-2=0(7分)
∵直线AB过椭圆的左焦点F∴方程有两个不等实根.(8分)
记A(x1,y1),B(x2,y2),AB的中点N(x0,y0)
则x1+x2=
| -4k2 |
| 1+2k2 |
x0=
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
垂直平分线NG的方程为y-y0=-
| 1 |
| k |
令y=0,得xG=x0+ky0=-
| 2k2 |
| 2k2+1 |
| k2 |
| 2k2+1 |
| k2 |
| 2k2+1 |
=-
| 1 |
| 2 |
| 1 |
| 4k2+2 |
∵k≠0,∴-
| 1 |
| 2 |
∴点G横坐标的取值范围为(-
| 1 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知椭圆
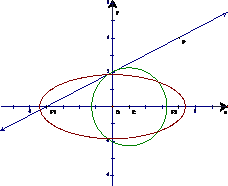
已知椭圆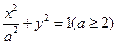 ,直线
,直线 与椭圆交于
与椭圆交于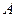 、
、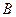 两点,
两点,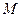 是线段
是线段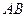 的中点,连接
的中点,连接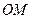 并延长交椭圆于点
并延长交椭圆于点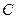 .
.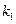 、
、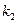 ,且
,且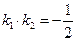 ,求椭圆的离心率.若直线
,求椭圆的离心率.若直线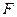 ,且四边形
,且四边形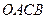 是平行四边形,求直线
是平行四边形,求直线