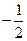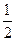题目内容

若直线mx+ny-5=0与圆x2+y2=5没有公共点，则过点P（m，n）的一条直线与椭圆
x2
7
+
y2
5
=1的公共点的个数是（　　）
A．0B．1C．2D．1或2
原点到直线mx+ny-5=0的距离d=
5
m2+n2
＞
5

∴m2+n2＜5
∴点P（m，n）是以原点为圆心，
5
为半径的圆内的点
∵椭圆的长半轴
7
，短半轴为
5

∴圆x2+y2=5内含于椭圆
∴点P是椭圆内的点
∴过点P（m，n）的一条直线与椭圆的公共点数为2
故选C
练习册系列答案
相关题目
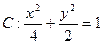已知椭圆和圆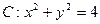，且圆C与x轴交于A1，A2两点（1）设椭圆C1的右焦点为F，点P的圆C上异于A1，A2的动点，过原点O作直线PF的垂线交椭圆的右准线交于点Q，试判断直线PQ与圆C的位置关系，并给出证明。  （2）设点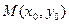在直线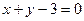上，若存在点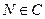，使得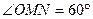（O为坐标原点），求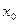的取值范围。
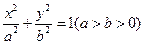椭圆C1：的左准线为l，左右焦点分别为F1、F­2，抛物线C2的准线为l，一个焦点为F2，C1与C2的一个交点为P，则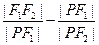等于（   ）
A．－1B．1C．D．
已知点P（4，4），圆C：（x-m）2+y2=5（m＜3）与椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)有一个公共点A（3，1），F1，F2分别是椭圆的左右焦点，直线PF1与圆C相切．
（1）求m的值；
（2）求椭圆E的方程．
已知中心在原点，顶点A1、A2在x轴上，离心率e=
21
3
的双曲线过点P（6，6）．
（1）求双曲线方程．
（2）动直线l经过△A1PA2的重心G，与双曲线交于不同的两点M、N，问：是否存在直线l，使G平分线段MN，证明你的结论．
若直线l被圆x2+y2=4所截得的弦长为2
3
，l与曲线
x2
3
+y2=1的公共点个数为（　　）
A．1个B．2个C．1个或2个D．1个或0个
己知斜率为1的直线l与双曲线C：
x2
a2
-
y2
b2
=1(a＞0，b＞0)相交于B、D两点，且BD的中点为M（1，3）．
（Ⅰ）求C的离心率；
（Ⅱ）设C的右顶点为A，右焦点为F，|DF|•|BF|=17，证明：过A、B、D三点的圆与x轴相切．
已知抛物线y=-
x2
2
与过点M（0，-1）的直线l相交于A、B两点，O为原点．若OA和OB的斜率之和为1．
（1）求直线l的方程；
（2）求△AOB的面积．
已知椭圆C1：
x2
2
+y2=1和圆C2：x2+y2=1，左顶点和下顶点分别为A，B，且F是椭圆C1的右焦点．
（1）若点P是曲线C2上位于第二象限的一点，且△APF的面积为
1
2
+
2
4
，求证：AP⊥OP；
（2）点M和N分别是椭圆C1和圆C2上位于y轴右侧的动点，且直线BN的斜率是直线BM斜率的2倍，求证：直线MN恒过定点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网