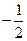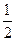题目内容
直线l:x-y=0与椭圆
+y2=1相交A、B两点,点C是椭圆上的动点,则△ABC面积的最大值为______.
| x2 |
| 2 |
直线l:x-y=0与椭圆
+y2=1联立,消元可得
=1,∴x=±
∴不妨设A(
,
),B(-
,-
)
∴|AB|=
设过C点且与AB平行的直线L方程为 y=x+c,L与AB距离就是C点到AB的距离,也就是三角形ABC的BC边上的高.
只要L与椭圆相切,就可得L与AB最大距离,可得最大面积.
y=x+c代入椭圆
+y2=1,消元可得3y2-2cy+c2-2=0
判别式△=4c2-12(c2-2)=0,∴c=±
∴L与AB最大距离为
=
∴△ABC最大面积:
×
×
=
故答案为:
| x2 |
| 2 |
| 3x2 |
| 2 |
| ||
| 3 |
∴不妨设A(
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
∴|AB|=
4
| ||
| 3 |
设过C点且与AB平行的直线L方程为 y=x+c,L与AB距离就是C点到AB的距离,也就是三角形ABC的BC边上的高.
只要L与椭圆相切,就可得L与AB最大距离,可得最大面积.
y=x+c代入椭圆
| x2 |
| 2 |
判别式△=4c2-12(c2-2)=0,∴c=±
| 3 |
∴L与AB最大距离为
| ||
|
| ||
| 2 |
∴△ABC最大面积:
| 1 |
| 2 |
4
| ||
| 3 |
| ||
| 2 |
| 2 |
故答案为:
| 2 |

练习册系列答案
相关题目
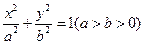 的左准线为l,左右焦点分别为F1、F2,抛物线C2的准线为l,一个焦点为F2,C1与C2的一个交点为P,则
的左准线为l,左右焦点分别为F1、F2,抛物线C2的准线为l,一个焦点为F2,C1与C2的一个交点为P,则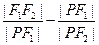 等于( )
等于( )