题目内容

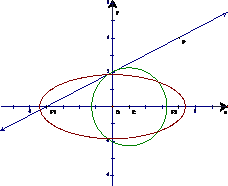
如图，A、B分别是椭圆
y2
a2
+
x2
b2
=1(a＞b＞0)的上、下两顶点，P是双曲线
y2
a2
-
x2
b2
=1上在第一象限内的一点，直线PA、PB分别交椭圆于C、D点，如果D恰是PB的中点．
（1）求证：无论常数a、b如何，直线CD的斜率恒为定值；
（2）求双曲线的离心率，使CD通过椭圆的上焦点．
（1）设P点坐标为（x0，y0），又A、B坐标分别是（0，a）、（0，-a）
而D是PB的中点，∴D点坐标为（
x0
2
，
y0-a
2
），
把D点坐标代入椭圆方程，得：
(y0-a)2
a2
+
x20
b2
=4 ①
又
y20
a2
-
x20
b2
=1 ②
由①②解得，y0=2a（y0=-a舍去）x0=
3
b，∴P点坐标为(
3
b，2a)
故kPA=
y0-a
x0
=
a
3
b
，直线PA的方程是y=
a
3
b
x+a与
y2
a2
+
x2
b2
=1联立，解得
C点坐标为(-
3
b
2
，
a
2
)，又D点坐标为(
3
2
b，
a
2
)
∴C、D两点关于y轴对称，故无论a、b如何变化，都有CD∥x轴，直线CD的斜率恒为常常0．
（2）当CD过椭圆焦点(0，
a2-b2
)时，
则
a2-b2
=
a
2
，∴b=
3
4
a2，
双曲线中，c=
a2+b2
=
7
2
a，
∴双曲线的离心率e=
c
a
=
7
2
．
练习册系列答案
相关题目
已知点P（4，4），圆C：（x-m）2+y2=5（m＜3）与椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)有一个公共点A（3，1），F1，F2分别是椭圆的左右焦点，直线PF1与圆C相切．
（1）求m的值；
（2）求椭圆E的方程．
已知抛物线y=-
x2
2
与过点M（0，-1）的直线l相交于A、B两点，O为原点．若OA和OB的斜率之和为1．
（1）求直线l的方程；
（2）求△AOB的面积．
设双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右焦点分别为F1，F2，且|F1F2|=4，一条渐近线的倾斜角为60°．
（I）求双曲线C的方程和离心率；
（Ⅱ）若点P在双曲线C的右支上，且△PF1F2的周长为16，求点P的坐标．
已知双曲线C的渐近线为y=±
3
x且过点M（1，
2
）．
（1）求双曲线C的方程；
（2）若直线y=ax+1与双曲线C相交于A，B两点，O为坐标原点，若OA与OB垂直，求a的值．
过抛物线y2=2px（p＞0）的焦点F作直线与抛物线交于A、B两点，以AB为直径的圆与抛物线的准线的位置关系是（　　）
A．相交B．相切
C．相离D．与p的取值相关
已知椭圆C1：
x2
2
+y2=1和圆C2：x2+y2=1，左顶点和下顶点分别为A，B，且F是椭圆C1的右焦点．
（1）若点P是曲线C2上位于第二象限的一点，且△APF的面积为
1
2
+
2
4
，求证：AP⊥OP；
（2）点M和N分别是椭圆C1和圆C2上位于y轴右侧的动点，且直线BN的斜率是直线BM斜率的2倍，求证：直线MN恒过定点．
已知定点A（2，2），M在抛物线x2=4y上，M在抛物线准线上的射影是P点，则MP-MA的最大值为（　　）
A．1B．
5
C．
7
D．5-2
2
已知直线l与椭圆C：
x2
3
+
y2
2
=1交于P（x1，y1），Q（x2，y2）两不同点，且△OPQ的面积S△OPQ=
6
2
，其中O为坐标原点．
（Ⅰ）证明x12+x22和y12+y22均为定值；
（Ⅱ）设线段PQ的中点为M，求|OM|•|PQ|的最大值；
（Ⅲ）椭圆C上是否存在点D，E，G，使得S△ODE=S△ODG=S△OEG=
6
2
？若存在，判断△DEG的形状；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网