题目内容
设数列 是有穷等差数列,给出下面数表:
是有穷等差数列,给出下面数表:


 ……
…… 
 第1行
第1行
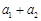
 ……
……  第2行
第2行
… … …
… …
… 第n行
上表共有行,其中第1行的个数为 ,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为
,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为 .
.
(1)求证:数列 成等比数列;
成等比数列;
(2)若 ,求和
,求和 .
.
 是有穷等差数列,给出下面数表:
是有穷等差数列,给出下面数表:

 ……
…… 
 第1行
第1行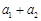
 ……
……  第2行
第2行… … …
… …
… 第n行
上表共有行,其中第1行的个数为
 ,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为
,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为 .
.(1)求证:数列
 成等比数列;
成等比数列;(2)若
 ,求和
,求和 .
.(1)根据等比数列的定义 ,证明从第二项起后一项与前一项的比值为定值即可。
(2)
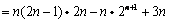
(2)

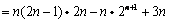
试题分析:(1)由题设易知,
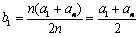 ,
,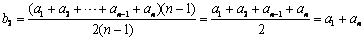 .
.设表中的第
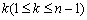 行的数为
行的数为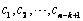 ,显然
,显然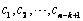 成等差数列,则它的第
成等差数列,则它的第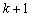 行的数是
行的数是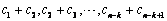 也成等差数列,它们的平均数分别是
也成等差数列,它们的平均数分别是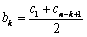 ,
,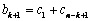 ,于是
,于是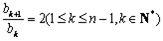 .
.故数列
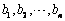 是公比为2的等比数列.
是公比为2的等比数列. (2)由(1)知,
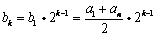 ,
,故当
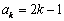 时,
时,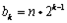 ,
,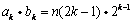
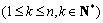 .
.于是
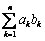
 .
.设
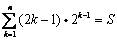 ,
,则
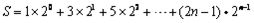 ①
①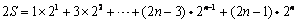 ②
②①
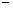 ②得,
②得,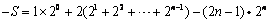 ,
,化简得,
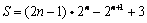 ,
,故
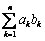
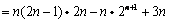 .
.点评:主要是考查了错位相减法求和的运用,属于易错题,注意准确的运算。

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
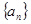 中,
中,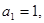 且点
且点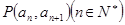 在直线
在直线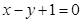 上。
上。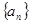 的通项公式;
的通项公式; (2)
(2)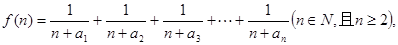 求函数
求函数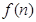 的最小值;
的最小值;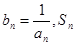 表示数列
表示数列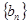 的前
的前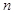 项和。试问:是否存在关于
项和。试问:是否存在关于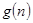 ,使得
,使得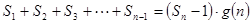 对于一切不小于2的自然数
对于一切不小于2的自然数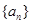 中,已知
中,已知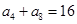 ,则该数列前11项和
,则该数列前11项和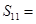 ( )
( ) 是一个等差数列,且
是一个等差数列,且 ,
, .
. ; (Ⅱ)求
; (Ⅱ)求 的通项
的通项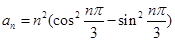 ,其前
,其前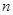 项和为
项和为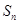 ,则
,则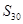 为 .
为 . 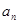 }的前n项和为
}的前n项和为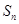 ,且
,且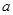 =1,
=1,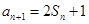 ,数列{
,数列{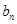 }满足
}满足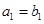 ,点P(
,点P(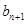 )在直线x―y+2=0上,
)在直线x―y+2=0上,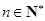 .
.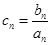 ,求数列{
,求数列{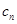 }的前n项和
}的前n项和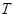 .
.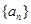 中,若
中,若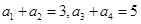 ,则
,则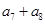 的和等于 ( )
的和等于 ( )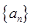 的前n项和为
的前n项和为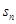 ,满足
,满足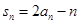
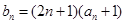 ,求数列
,求数列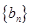 的前n项和
的前n项和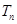 。
。