题目内容
(本题满分14分)
设数列{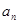 }的前n项和为
}的前n项和为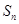 ,且
,且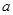 =1,
=1,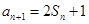 ,数列{
,数列{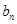 }满足
}满足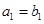 ,点P(
,点P(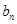 ,
,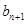 )在直线x―y+2=0上,
)在直线x―y+2=0上,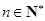 .
.
(1)求数列{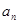 },{
},{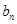 }的通项公式;
}的通项公式;
(2)设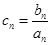 ,求数列{
,求数列{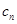 }的前n项和
}的前n项和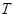 .
.
设数列{
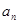 }的前n项和为
}的前n项和为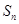 ,且
,且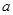 =1,
=1,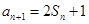 ,数列{
,数列{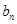 }满足
}满足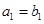 ,点P(
,点P(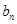 ,
,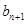 )在直线x―y+2=0上,
)在直线x―y+2=0上,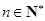 .
.(1)求数列{
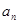 },{
},{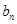 }的通项公式;
}的通项公式;(2)设
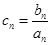 ,求数列{
,求数列{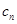 }的前n项和
}的前n项和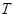 .
.(1)
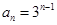 ,
,
(2)
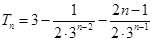
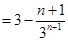 .
.试题分析:解:(1)由
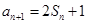 可得
可得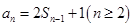 ,两式相减得
,两式相减得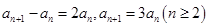 .
.又
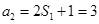 ,所以
,所以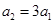 .
. 故
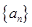 是首项为,公比为
是首项为,公比为 的等比数列.所以
的等比数列.所以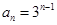 .
. 由点
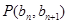 在直线
在直线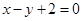 上,所以
上,所以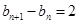 .
.则数列
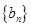 是首项为1,公差为2的等差数列.则
是首项为1,公差为2的等差数列.则
(2)因为
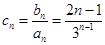 ,所以
,所以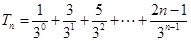 .
. 则
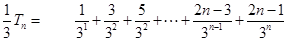 ,
, 两式相减得:
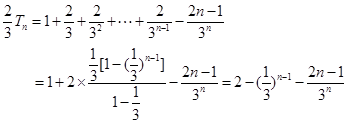
所以
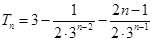
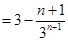 .
. 点评:结合等差数列和等比数列的基本量求解通项公式,同时利用错位相减法求解和,属于基础题。

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 =
= ,则
,则 =( ).
=( ).
 是有穷等差数列,给出下面数表:
是有穷等差数列,给出下面数表:

 ……
…… 
 第1行
第1行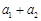
 ……
……  第2行
第2行 ,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为
,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为 .
. ,求和
,求和 .
. ,
, ,
, ,则
,则 的值为( )。
的值为( )。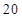 的样本数据,它们组成一个公差不为
的样本数据,它们组成一个公差不为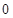 的等差数列
的等差数列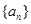 ,若
,若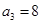 且前
且前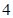 项和
项和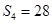 ,则此样本的平均数和中位数分别是
,则此样本的平均数和中位数分别是 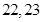
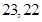
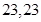
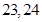
 的前
的前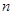 项和为
项和为 ,满足
,满足 .
. 为等比数列;
为等比数列; 满足
满足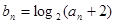 ,
, 为数列
为数列 的前
的前 .
.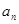 }的前n项和为Sn,且
}的前n项和为Sn,且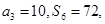
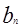 =
=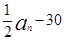
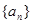 的前
的前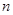 项和为
项和为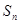 ,且
,且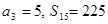 .
.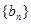 满足:
满足: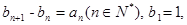 求数列
求数列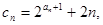 求数列
求数列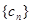 的前
的前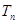 .
.