题目内容
已知 是一个等差数列,且
是一个等差数列,且 ,
, .
.
(Ⅰ)求 的通项
的通项 ; (Ⅱ)求
; (Ⅱ)求 前n项和Sn的最大值.
前n项和Sn的最大值.
 是一个等差数列,且
是一个等差数列,且 ,
, .
.(Ⅰ)求
 的通项
的通项 ; (Ⅱ)求
; (Ⅱ)求 前n项和Sn的最大值.
前n项和Sn的最大值.(1)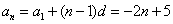 (2)
(2) 时,
时, 取到最大值
取到最大值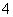
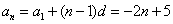 (2)
(2) 时,
时, 取到最大值
取到最大值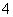
试题分析:(Ⅰ)设
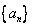 的公差为
的公差为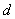 ,由已知条件,
,由已知条件,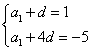 ,解出
,解出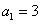 ,
, .
.所以
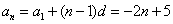 .
.(Ⅱ)

 .所以
.所以 时,
时, 取到最大值
取到最大值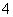 .
.点评:考查了等差数列的通项公式和前n项和的最值的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
 是一个等差数列,且
是一个等差数列,且 ,
, .
. 的通项
的通项 ; (Ⅱ)求
; (Ⅱ)求 前n项和Sn的最大值.
前n项和Sn的最大值.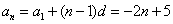 (2)
(2) 时,
时, 取到最大值
取到最大值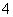
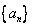 的公差为
的公差为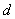 ,由已知条件,
,由已知条件,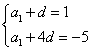 ,解出
,解出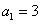 ,
, .
.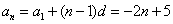 .
.
 .所以
.所以 时,
时, 取到最大值
取到最大值 .
.
 阅读快车系列答案
阅读快车系列答案