题目内容
已知二次函数f(x)=ax2+bx(a≠0),且f(x+1)为偶函数,定义:满足f(x)=x的实数x称为函数f(x)的“不动点”,若函数f(x)有且仅有一个不动点.
(1)求f(x)的解析式;
(2)若函数g(x)=f(x)+kx2在(0,4)上是增函数,求实数k的取值范围;
(3)是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域为[3m,3n]?若存在,请求出m,n的值;若不存在,请说明理由.
(1)求f(x)的解析式;
(2)若函数g(x)=f(x)+kx2在(0,4)上是增函数,求实数k的取值范围;
(3)是否存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域为[3m,3n]?若存在,请求出m,n的值;若不存在,请说明理由.
(1)由题意可得,二次函数f(x)=ax2+bx(a≠0)的对称轴为x=-
=1,
∴b=-2a,
f(x)=ax2 -2ax.
再根据函数f(x)有且仅有一个不动点,可得ax2 -2ax=x只有一个解,
故△=(2a+1)2-0=0,
∴a=-
,b=1
∴f(x)=-
x2+x
(2)∵函数g(x)=f(x)+kx2=(k-
)x2+x
当k-
=0,即k=
时,
g(x)=x在(0,4)上是增函数,满足要求;
当k-
>0,即k>
时,
若g(x)=x在(0,4)上是增函数,
则
≤0,解得k>
,
当k-
<0,即k<
时,
若g(x)=x在(0,4)上是增函数,
则
≥4,解得
≤k<
,
综上所述,实数k的取值范围为[
,+∞)
(3)f(x)=-
x2+x=-
(x-1)2+
≤
∵f(x)在区间[m,n]上的值域为[3m,3n]
∴3n≤
∴n≤
故m<n≤
∴f(x)在区间[m,n]上为增函数
∴
即
即m,n为方程-
x2+x=3x的两根,
解-
x2+x=3x得x=-4,或x=0
故m=-4,n=0
| b |
| 2a |
∴b=-2a,
f(x)=ax2 -2ax.
再根据函数f(x)有且仅有一个不动点,可得ax2 -2ax=x只有一个解,
故△=(2a+1)2-0=0,
∴a=-
| 1 |
| 2 |
∴f(x)=-
| 1 |
| 2 |
(2)∵函数g(x)=f(x)+kx2=(k-
| 1 |
| 2 |
当k-
| 1 |
| 2 |
| 1 |
| 2 |
g(x)=x在(0,4)上是增函数,满足要求;
当k-
| 1 |
| 2 |
| 1 |
| 2 |
若g(x)=x在(0,4)上是增函数,
则
| 1 |
| 1-2k |
| 1 |
| 2 |
当k-
| 1 |
| 2 |
| 1 |
| 2 |
若g(x)=x在(0,4)上是增函数,
则
| 1 |
| 1-2k |
| 3 |
| 8 |
| 1 |
| 2 |
综上所述,实数k的取值范围为[
| 3 |
| 8 |
(3)f(x)=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵f(x)在区间[m,n]上的值域为[3m,3n]
∴3n≤
| 1 |
| 2 |
∴n≤
| 1 |
| 6 |
故m<n≤
| 1 |
| 6 |
∴f(x)在区间[m,n]上为增函数
∴
|
即
|
即m,n为方程-
| 1 |
| 2 |
解-
| 1 |
| 2 |
故m=-4,n=0

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

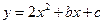 在
在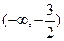 上是减函数,在
上是减函数,在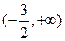 上是增函数,且两个零点
上是增函数,且两个零点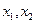 满足
满足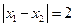 ,求二次函数的解析式。
,求二次函数的解析式。