题目内容
已知函数f（x）=2x-x2，x∈[4，5]，对于f（x）值域内的所有实数m，满足不等式t2+mt+4＞2m+4t恒成立t的集合是（ ）
| A．（-∞，-5） | B．（-∞，-2）∪（5，+∞） |
| C．（-∞，-5）∪（2，+∞） | D．（-∞，-5）∪（-2，+∞） |
f′（x）=2xln2-2x，[f′（x）]′=2xln22-2，
因为ln2＞ln
=
，所以当x≥4时，[f′（x）]′=2xln22-2≥24ln22-2＞0，
故f′（x）在[4，5]上递增，且f′（x）≥f′（4）=24ln2-2×4＞0，
所以f（x）在[4，5]上递增，所以f（x）min=f（4）=0，f（x）max=f（5）=7，即m∈[0，7]．
t2+mt+4＞2m+4t恒成立即（t-2）m+t2-4t+4＞0对任意m∈[0，7]恒成立，令g（m）=（t-2）m+t2-4t+4，
则有
，即
，解得t＜-5，或t＞2，
故选C．
因为ln2＞ln
| e |
| 1 |
| 2 |
故f′（x）在[4，5]上递增，且f′（x）≥f′（4）=24ln2-2×4＞0，
所以f（x）在[4，5]上递增，所以f（x）min=f（4）=0，f（x）max=f（5）=7，即m∈[0，7]．
t2+mt+4＞2m+4t恒成立即（t-2）m+t2-4t+4＞0对任意m∈[0，7]恒成立，令g（m）=（t-2）m+t2-4t+4，
则有
|
|
故选C．
练习册系列答案
阅读快车系列答案
相关题目
；
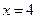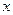轴两个交点的横坐标都是整数；
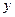轴交点的纵坐标也是整数，且以这三个交点为顶点的三角形面积为
．
，
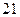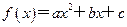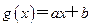，当
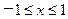时，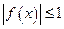
．
；
；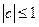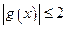