题目内容
1.在坐标平面内,与点A(1,1)距离为1,且与点B(4,1)距离为2的直线共有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
分析 问题转化为两圆的公切线条数,判断圆的位置关系可得.
解答 解:在坐标平面内,与点A(1,1)距离为1的直线为圆(x-1)2+(y-1)2=1的切线,
同理可得在坐标平面内,与点B(4,1)距离为2的直线为圆(x-4)2+(y-1)2=4的切线,
故所求直线为两圆的公切线,
∵|AB|=$\sqrt{(1-4)^{2}+(1-1)^{2}}$=3=1+2,
∴两圆外切,公切线由3条,
故选:C.
点评 本题考查点到直线的距离,转化为两圆的公切线是解决问题的关键,属基础题.

练习册系列答案
相关题目
6.一个商场经销某种商品,根据以往资料统计,每位顾客采用的分期付款次数ξ的分布列为:
商场经销一件该商品,采用1期付款,其利润为200元;采用2期或3期付款,其利润为250元;采用4期或5期付款,其利润为300元.η表示经销一件该商品的利润.
(1)求购买该商品的3位顾客中,恰有2位采用1期付款的概率;
(2)求η的分布列及期望E(η).
| ξ | 1 | 2 | 3 | 4 | 5 |
| P | 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
(1)求购买该商品的3位顾客中,恰有2位采用1期付款的概率;
(2)求η的分布列及期望E(η).
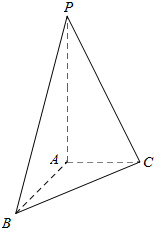 如图,在三棱锥P-ABC中,PA丄平面ABC,AC丄AB,PA=AB=2,AC=1.
如图,在三棱锥P-ABC中,PA丄平面ABC,AC丄AB,PA=AB=2,AC=1. 如图,圆O的半径为2,P是圆O的直径AB延长线上的一点,BP=1,割线PCD交圆O于C、D两点,过P作FP⊥AP,交直线AC于点E,交直线AD于点F.
如图,圆O的半径为2,P是圆O的直径AB延长线上的一点,BP=1,割线PCD交圆O于C、D两点,过P作FP⊥AP,交直线AC于点E,交直线AD于点F. 如图,已知A(10,0),直线x=t(0<t<10)与函数y=ex的图象交于点P,与x轴交于点H,记△APH的面积为f(t).
如图,已知A(10,0),直线x=t(0<t<10)与函数y=ex的图象交于点P,与x轴交于点H,记△APH的面积为f(t).