题目内容
9.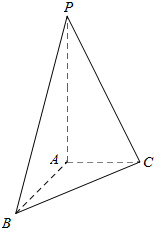 如图,在三棱锥P-ABC中,PA丄平面ABC,AC丄AB,PA=AB=2,AC=1.
如图,在三棱锥P-ABC中,PA丄平面ABC,AC丄AB,PA=AB=2,AC=1.(Ⅰ) 证明:PC丄AB;
(Ⅱ)求二面角A-PC-B的正弦值;
(Ⅲ) 求三棱锥P-ABC外接球的体积.
分析 (Ⅰ)证明AB⊥平面PC,即可证明:PC丄AB;
(Ⅱ)过A作AM⊥PC交PC于点M,连接BM,则∠AMB为所求角,即可求二面角A-PC-B的正弦值;
(Ⅲ)求三棱锥P-ABC外接球即为以AP,AB,AC为棱的长方体的外接球,长方体的对角线为球的直径,可求三棱锥P-ABC外接球的体积.
解答 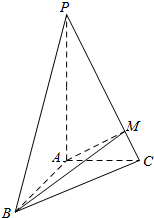 (Ⅰ)证明:$\left.\begin{array}{l}AB⊥AC\\ AB⊥PA\end{array}\right\}⇒AB⊥平面PAC⇒AB⊥PC$;…(4分)
(Ⅰ)证明:$\left.\begin{array}{l}AB⊥AC\\ AB⊥PA\end{array}\right\}⇒AB⊥平面PAC⇒AB⊥PC$;…(4分)
(Ⅱ)解:过A作AM⊥PC交PC于点M,连接BM,则∠AMB为所求角;…(6分)
在三角形AMB中,$sin∠AMB=\frac{AB}{BM}=\frac{{\sqrt{30}}}{6}$…(8分)
(Ⅲ)解:求三棱锥P-ABC外接球即为以AP,AB,AC为棱的长方体的外接球,长方体的对角线为球的直径,…(10分)
${l^2}={2^2}+{2^2}+{1^2}=9={(2R)^2}⇒R=\frac{3}{2}$$V=\frac{4}{3}π{R^3}=\frac{4}{3}π×{(\frac{3}{2})^3}=\frac{9}{2}π$.…(12分)
点评 本题考查线面垂直的证明,考查二面角,考查三棱锥P-ABC外接球体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
19.已知袋中装有标号为1,2,3的三个小球,从中任取一个小球(取后放回),连取三次,则取到的小球的最大标号为3的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{19}{27}$ | C. | $\frac{20}{27}$ | D. | $\frac{7}{9}$ |
20.函数f(x)=2x3-4x 的单调递减区间是( )
| A. | (-$\sqrt{6}$,$\sqrt{6}$) | B. | (-$\frac{\sqrt{2}}{3}$,$\frac{\sqrt{2}}{3}$) | C. | (-$\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$) | D. | (-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$) |
1.在坐标平面内,与点A(1,1)距离为1,且与点B(4,1)距离为2的直线共有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
18.一个几何体的三视图如图所示,则该几何体的表面积为( )


| A. | $\frac{2π}{3}$ | B. | π | C. | 2π | D. | 3π |
19.“x<2”是“x(x-1)<0”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
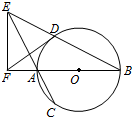 如图AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.
如图AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.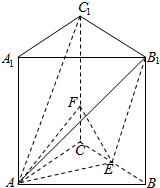 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=BC=AC=AA1=4,点F在CC1上,且C1F=3FC,E是BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=BC=AC=AA1=4,点F在CC1上,且C1F=3FC,E是BC的中点.