题目内容
16. 如图,圆O的半径为2,P是圆O的直径AB延长线上的一点,BP=1,割线PCD交圆O于C、D两点,过P作FP⊥AP,交直线AC于点E,交直线AD于点F.
如图,圆O的半径为2,P是圆O的直径AB延长线上的一点,BP=1,割线PCD交圆O于C、D两点,过P作FP⊥AP,交直线AC于点E,交直线AD于点F.(1)求证:∠PEC=∠PDF;
(2)求PE•PF的值.
分析 (1)连结BD,则∠BDA=90°,利用∠CDB=∠CAB,即可证明结论;
(2)利用割线定理,即可求出PE•PF的值.
解答  (1)证明:连结BD,则∠BDA=90°…(1分)
(1)证明:连结BD,则∠BDA=90°…(1分)
∵∠CDB=∠CAB…(2分)
∠PEC=90°-∠CAB,…(3分)
∠PDF=90°-∠CDB…(4分)
∴∠PEC=∠PDF…(5分)
(2)解:由(1)得:∠PEC=∠PDF,
∴D,C,E,F四点共圆,…(7分)
∴PE•PF=PC•PD=PB•PA=1×5=5…(10分)
点评 本题考查四点共圆是证明,考查割线定理的运用,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
相关题目
7.下列说法中正确的是( )
| A. | 若a>b,则$\sqrt{a}$>$\sqrt{b}$ | B. | 若|a|>b,则a2>b2 | C. | 若a>b,则a2>b2 | D. | 若a>|b|,则a2>b2 |
1.在坐标平面内,与点A(1,1)距离为1,且与点B(4,1)距离为2的直线共有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
8.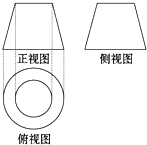 如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
 如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )| A. | 6π | B. | 12π | C. | 18π | D. | 24π |
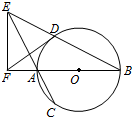 如图AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.
如图AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.