题目内容
10.已知函数f(x)=asinx+cosx的图象经过点$(\frac{π}{2},-1)$.(1)求函数f(x)的最小正周期与单调递增区间.
(2)若$θ∈({0,\frac{π}{2}})$,且f(θ)=$\frac{1}{2}$,求sin2θ的值.
分析 (1)由题意f($\frac{π}{2}$)=-1,解得a的值,由三角函数恒等变换化简可得解析式f(x)=$\sqrt{2}$cos(x+$\frac{π}{4}$),利用周期公式可求最小正周期,由2kπ-π≤x$+\frac{π}{4}$≤2kπ解得单调递增区间.
(2)解法1:由f(θ)=$\frac{1}{2}$,可得cos($θ+\frac{π}{4}$)=$\frac{\sqrt{2}}{4}$.利用sin2θ=-cos($\frac{π}{2}+2θ$)=1-2cos2($θ+\frac{π}{4}$)即可得解.
解法2:由f(θ)=$\frac{1}{2}$,可得$\sqrt{2}cos(θ+\frac{π}{4})$=$\frac{1}{2}$.由两角和的余弦函数公式可求cos$θ-sinθ=\frac{1}{2}$,两边平方由二倍角公式即可得解.
解答 解:(1)因为函数f(x)=asinx+cosx的图象经过点$(\frac{π}{2},-1)$,
所以f($\frac{π}{2}$)=-1,…(1分)
即asin$\frac{π}{2}$+cos$\frac{π}{2}$=-1,解得:a=-1,…(2分)
f(x)=cosx-sinx=$\sqrt{2}$cos(x+$\frac{π}{4}$),…(4分)
T=$\frac{2π}{1}=2π$,所以函数f(x)的最小正周期为2π. …(5分)
因为函数y=cosx的单调递增区间为[2kπ-π,2kπ],k∈Z,
所以2kπ-π≤x$+\frac{π}{4}$≤2kπ 解得:-$\frac{5π}{4}+2kπ$≤x≤2k$π-\frac{π}{4}$…(6分)
所以函数f(x)的单调递增区间为[-$\frac{5π}{4}+2kπ$,2k$π-\frac{π}{4}$],k∈Z …(7分)
(2)解法1:∵f(θ)=$\frac{1}{2}$,
∴$\sqrt{2}cos(θ+\frac{π}{4})$=$\frac{1}{2}$.
∴cos($θ+\frac{π}{4}$)=$\frac{\sqrt{2}}{4}$.…(9分)
∴sin2θ=-cos($\frac{π}{2}+2θ$)=1-2cos2($θ+\frac{π}{4}$)=1-2×($\frac{\sqrt{2}}{4}$)2=$\frac{3}{4}$.…(12分)
解法2:∵f(θ)=$\frac{1}{2}$,∴$\sqrt{2}cos(θ+\frac{π}{4})$=$\frac{1}{2}$.
∴$\sqrt{2}(cosθcos\frac{π}{4}-sinθsin\frac{π}{4})=\frac{1}{2}$.
∴cos$θ-sinθ=\frac{1}{2}$.…(9分)
两边平方得cos2θ-2cosθsinθ+sin2θ=$\frac{1}{4}$.…(11分)
∴sin2θ=$\frac{3}{4}$.…(12分)
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,二倍角公式的应用,正弦函数的图象和性质,三角函数恒等变换的应用,属于基本知识的考查.

| A. | (-$\sqrt{6}$,$\sqrt{6}$) | B. | (-$\frac{\sqrt{2}}{3}$,$\frac{\sqrt{2}}{3}$) | C. | (-$\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$) | D. | (-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$) |
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |

| A. | $\frac{2π}{3}$ | B. | π | C. | 2π | D. | 3π |
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
| A. | 1 | B. | -1 | C. | 1或-1 | D. | ±1或0 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
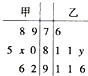 某中学高一级从甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是80,乙班学生成绩的中位数是89,则x+y的值为( )
某中学高一级从甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是80,乙班学生成绩的中位数是89,则x+y的值为( )