题目内容
13.设l,m是两条不同的直线,α,β是两个不重合的平面,给出下列四个命题:①若α∥β,l⊥α,则l⊥β; ②若l∥m,l?α,m?β,则α∥β;
③若m⊥α,l⊥m,则l∥α; ④若α⊥β,l?α,m?β,则l⊥m.
其中真命题的序号为①.
分析 ①根据一条直线与两个平行平面中的一个垂直,那么它与另一个平面垂直,即可判断正误;
②根据两个平面平行的判断方法即可判断正误;
③根据直线与平面平行的判断方法,得出命题错误;
④根据两个平面垂直的性质定理,即可判断命题错误.
解答 解:对于①,当α∥β时,若l⊥α,则l⊥β,
理由是如果一条直线与两个平行平面中的一个垂直,那么它与另一个平面垂直,∴①正确;
对于②,当l∥m,l?α,m?β时,α∥β或α与β相交,∴②错误;
对于③,当m⊥α,l⊥m时,l∥α或l?α,∴③错误;
对于④,当α⊥β,l?α,m?β时,l⊥m或l与m不垂直,∴④错误.
综上,正确的命题是①.
故答案为:①.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了几何符号语言与空间想象能力的应用问题.

练习册系列答案
相关题目
1.在坐标平面内,与点A(1,1)距离为1,且与点B(4,1)距离为2的直线共有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
8.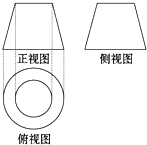 如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
 如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )
如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )| A. | 6π | B. | 12π | C. | 18π | D. | 24π |
18.一个几何体的三视图如图所示,则该几何体的表面积为( )


| A. | $\frac{2π}{3}$ | B. | π | C. | 2π | D. | 3π |
2.已知i为虚数单位,复数z1=a+2i,z2=2-i,且|z1|=|z2|,则实数a的值为( )
| A. | 1 | B. | -1 | C. | 1或-1 | D. | ±1或0 |
3.用三段论推理:“对数函数y=logax(a>0且a≠1)在(0,+∞)上是减函数,因为y=log2x是对数函数,所以y=log2x在(0,+∞)上是减函数”,你认为这个推理( )
| A. | 大前提错误 | B. | 小前提错误 | ||
| C. | 推理形式错误 | D. | 大前提和小前提都错误 |
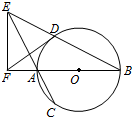 如图AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.
如图AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.