��Ŀ����
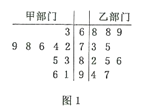
����Ŀ��ijУ�߶��꼶�����˰ٿ�֪ʶ������Ϊ���˽�߶��꼶900��ͬѧ�ı�����������ڼס��������༶�������ȡ��10��ͬѧ�ijɼ��������ɼ�����Ϊ100�֣�80�����Ͽɻ�ö��Ƚ���90�����Ͽ��Ի��һ�Ƚ�����֪��ȡ��������ѧ���ijɼ�����λ���֣����ݵľ�Ҷͼ��ͼ1��ʾ:

��1���Ƚ��������ݵķ�ɢ�̶ȣ�ֻ��Ҫ�������ۣ���������������ݵ�Ƶ�ʷֲ�ֱ��ͼ��ͼ2����ʾ��![]() ֵ��
ֵ��
��2���ִ����������л�ѧ����ֱ������ȡһ�˽��ܲɷã����еļװ�ѧ���ɼ������Ұ�ѧ���ɼ��ĸ���.
���𰸡���1���������ݸ�����,�������ݸ���ɢ�� ![]() =0.05��
=0.05�� ![]() =0.02��
=0.02�� ![]() =0.01.��2��
=0.01.��2��![]()
�������������������1���������ݼ��г̶�ȷ����ɢ�̶�,����Ƶ�ʵ���Ƶ�����������ö�Ӧ�������,�ٳ�������![]() ֵ����2���װ��4�ˣ��Ұ��5�ˣ��������¼���Ϊ
ֵ����2���װ��4�ˣ��Ұ��5�ˣ��������¼���Ϊ![]() ,���мװ�ѧ���ɼ������Ұ�ѧ���ɼ����¼�����9��(ö�ٷ�),�����ݹŵ�������������
,���мװ�ѧ���ɼ������Ұ�ѧ���ɼ����¼�����9��(ö�ٷ�),�����ݹŵ�������������
�����������I���ɾ�Ҷͼ��֪,�������ݸ�����,�������ݸ���ɢ![]() =0.05��
=0.05�� ![]() =0.02��
=0.02�� ![]() =0.01.
=0.01.
��II���ɾ�Ҷͼ֪���װ��4�ˣ��Ұ��5�ˣ�����![]() .
.

��ϰ��ϵ�д�
 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�
�����Ŀ