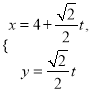题目内容
【题目】已知点![]() 在圆
在圆![]() :
: ![]() 上,而
上,而![]() 为
为![]() 在
在![]() 轴上的投影,且点
轴上的投影,且点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 是曲线
是曲线![]() 上两点,且
上两点,且![]() ,
, ![]() 为坐标原点,求
为坐标原点,求![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:
由![]() 可知,N为中点,用相关点法可以求出N点的轨迹方程。
可知,N为中点,用相关点法可以求出N点的轨迹方程。
分斜率存在和不存在讨论,当斜率存在时,设直线![]() 方程为:
方程为: ![]() ,与椭圆组方程组,利用弦长公式和韦达定理建立k,t的关系式。再利用点到直线的距离公式和面积公式用k,t表示三角形面积,消t,换元可解。
,与椭圆组方程组,利用弦长公式和韦达定理建立k,t的关系式。再利用点到直线的距离公式和面积公式用k,t表示三角形面积,消t,换元可解。
试题解析:
(1)设![]() ,
, ![]() 轴,所以
轴,所以![]()
又设![]() ,由
,由![]() 有
有![]() 代入
代入![]() 即曲线
即曲线![]() 的方程为
的方程为![]()
(2)设![]() ,
, ![]() ,直线
,直线![]() 方程为:
方程为: ![]() ,
,
联立![]() 得
得![]() ,故
,故![]() ,
,
由4![]() ,得
,得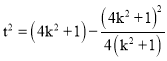 ,
,
故原点![]() 到直线
到直线![]() 的距离
的距离![]() ,∴
,∴![]() ,
,
令![]() ,则
,则![]() ,又∵
,又∵![]() , 当
, 当![]() .
.
当斜率不存在时, ![]() 不存在,综合上述可得
不存在,综合上述可得![]() 面积的最大值为1.
面积的最大值为1.

练习册系列答案
相关题目