题目内容
15.已知f(x)=sin2(x+$\frac{π}{4}$)+2若a=f(lg5),b=f(lg$\frac{1}{5}$),则a+b=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 首先对f(x)利用倍角公式化简为$\frac{5}{2}$+$\frac{1}{2}$sin2x,又因为lg$\frac{1}{5}$=-lg5,代入解析式得到所求.
解答 解:由已知f(x)=sin2(x+$\frac{π}{4}$)+2=$\frac{5}{2}$-$\frac{1}{2}$cos(2x+$\frac{π}{2}$)=$\frac{5}{2}+\frac{1}{2}sin2x$,又a=f(lg5),b=f(lg$\frac{1}{5}$),
所以a+b=5+$\frac{1}{2}$sin(2lg5)+$\frac{1}{2}$sin(2lg$\frac{1}{5}$)=5+$\frac{1}{2}$sin(2lg5)+$\frac{1}{2}$sin(-2lg5)=5;
故选:C.
点评 本题考查了三角函数的倍角公式、诱导公式、互为倒数的两个正数的同底数的对数互为相反数;注意符号.

练习册系列答案
相关题目
5.甲有三本不同的书,乙去借阅,且至少借1本,则不同借法的总数为( )
| A. | 3 | B. | 6 | C. | 7 | D. | 9 |
6.如图⊙O中,弦AB与弦CD相交于点P,∠B=38°,∠APD=80°,则∠A等于( )
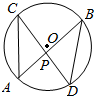

| A. | 38° | B. | 42° | C. | 80° | D. | 118° |
3.设(x+3)(2x+3)10=a0+a1(x+3)+a2(x+3)2+…+a11(x+3)11,则a0+a1+a2+…+a11的值为( )
| A. | 1 | B. | 2 | C. | 311 | D. | 4×510 |
20.下列说法正确的是( )
| A. | 如果两个复数的实部的差和虚部的差都等于0,那么这两个复数相等 | |
| B. | ai是纯虚数(a∈R) | |
| C. | 如果复数x+yi(x,y∈R)是实数,则x=0,y=0 | |
| D. | 复数a+bi(a,b∈R)不是实数 |
4.把13个相同的球全部放入编号为1、2、3的三个盒内,要求盒内的球数不小于盒号数,则不同的放入方法种数为( )
| A. | 36 | B. | 45 | C. | 66 | D. | 78 |
5.研究一下,满足以下两个要求的三角形:①三边是连续的三个自然数;②最大角是最小角的两倍.这样的三角形( )
| A. | 不存在 | B. | 可能是直角三角形 | ||
| C. | 必为钝角三角形 | D. | 可能是锐角三角形 |