题目内容
已知点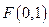 ,直线
,直线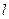 :
: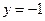 ,
,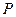 为平面上的动点,过点
为平面上的动点,过点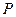 作直线
作直线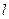 的垂线,垂足为
的垂线,垂足为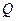 ,且
,且 .
.
(1)求动点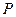 的轨迹
的轨迹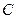 的方程;
的方程;
(2)已知圆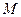 过定点
过定点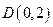 ,圆心
,圆心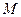 在轨迹
在轨迹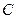 上运动,且圆
上运动,且圆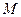 与
与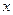 轴交于
轴交于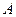 、
、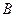 两点,设
两点,设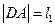 ,
, ,求
,求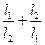 的最大值.
的最大值.
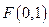 ,直线
,直线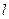 :
: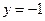 ,
,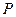 为平面上的动点,过点
为平面上的动点,过点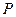 作直线
作直线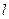 的垂线,垂足为
的垂线,垂足为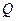 ,且
,且 .
.(1)求动点
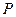 的轨迹
的轨迹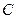 的方程;
的方程;(2)已知圆
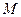 过定点
过定点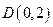 ,圆心
,圆心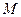 在轨迹
在轨迹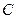 上运动,且圆
上运动,且圆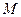 与
与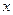 轴交于
轴交于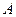 、
、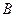 两点,设
两点,设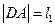 ,
, ,求
,求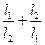 的最大值.
的最大值.(1) 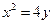 (2)当
(2)当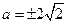 时,
时,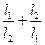 的最大值为
的最大值为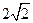
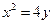 (2)当
(2)当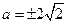 时,
时,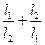 的最大值为
的最大值为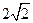
(1)解:设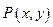 ,则
,则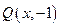 ,
,
∵ ,
,
∴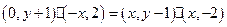 .
.
即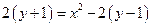 ,即
,即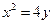 ,
,
所以动点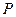 的轨迹
的轨迹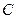 的方程
的方程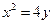 .
.
(2)解:设圆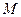 的圆心坐标为
的圆心坐标为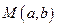 ,则
,则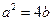 . ①
. ①
圆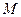 的半径为
的半径为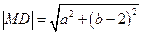 .
.
圆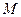 的方程为
的方程为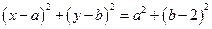 .
.
令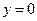 ,则
,则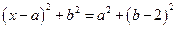 ,
,
整理得,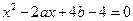 . ②
. ②
由①、②解得,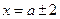 .
.
不妨设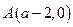 ,
,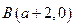 ,
,
∴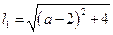 ,
,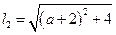 .
.
∴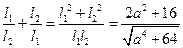
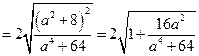 , ③
, ③
当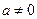 时,由③得,
时,由③得,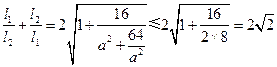 .
.
当且仅当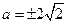 时,等号成立.
时,等号成立.
当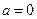 时,由③得,
时,由③得,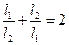 .
.
故当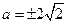 时,
时,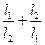 的最大值为
的最大值为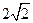 .
.
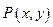 ,则
,则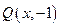 ,
,∵
 ,
,∴
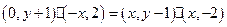 .
. 即
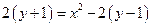 ,即
,即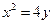 ,
,所以动点
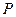 的轨迹
的轨迹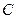 的方程
的方程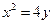 .
. (2)解:设圆
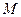 的圆心坐标为
的圆心坐标为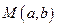 ,则
,则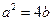 . ①
. ①圆
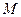 的半径为
的半径为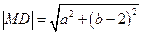 .
. 圆
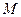 的方程为
的方程为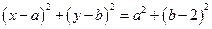 .
.令
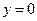 ,则
,则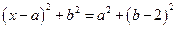 ,
,整理得,
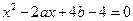 . ②
. ②由①、②解得,
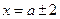 .
. 不妨设
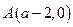 ,
,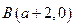 ,
,∴
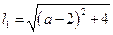 ,
,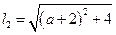 .
.∴
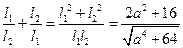
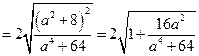 , ③
, ③当
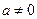 时,由③得,
时,由③得,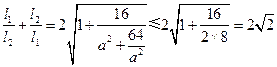 .
. 当且仅当
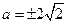 时,等号成立.
时,等号成立.当
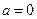 时,由③得,
时,由③得,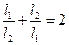 .
. 故当
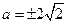 时,
时,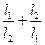 的最大值为
的最大值为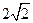 .
. 
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
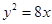 的焦点到双曲线
的焦点到双曲线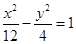 的渐近线的距离为( )
的渐近线的距离为( )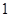
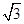
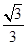
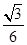
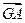 +
+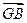 +
+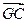 =0;②|
=0;②|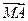 |=|
|=|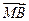 |=|
|=|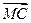 |;③
|;③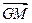 ∥
∥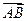 .(Ⅰ)求△ABC的顶点C的轨迹方程;(Ⅱ)是否存在过点P(3,0)的直线l与(Ⅰ)中轨迹交于E、F两点,且OE⊥OF?若存在,求出直线l斜率k的值;若不存在,说明理由.
.(Ⅰ)求△ABC的顶点C的轨迹方程;(Ⅱ)是否存在过点P(3,0)的直线l与(Ⅰ)中轨迹交于E、F两点,且OE⊥OF?若存在,求出直线l斜率k的值;若不存在,说明理由.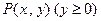 到定点
到定点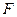
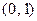 的距离比它到
的距离比它到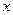 轴的距离大1,记点
轴的距离大1,记点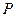 的轨迹为曲线
的轨迹为曲线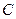 .
.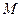 过
过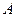
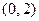 ,且圆心
,且圆心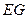 是圆
是圆 是否为定值?为什么?
是否为定值?为什么?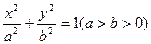 的左焦点为F,上顶点为A,过点A作垂直于AF的直线交椭圆C于另外一点P,交x轴正半轴于点Q,且
的左焦点为F,上顶点为A,过点A作垂直于AF的直线交椭圆C于另外一点P,交x轴正半轴于点Q,且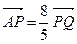
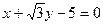 相切,求椭圆C的方程.
相切,求椭圆C的方程. 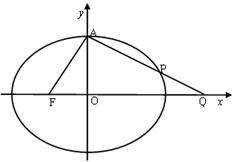
 相切,过点P(-4,0)作斜率为
相切,过点P(-4,0)作斜率为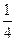 的直线l,使得l和G交于A、B两点,和y轴交于点C,并且点P在线段AB上,又满足
的直线l,使得l和G交于A、B两点,和y轴交于点C,并且点P在线段AB上,又满足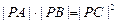
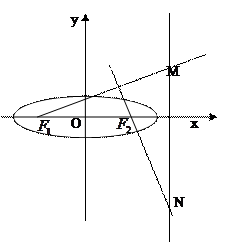 设椭圆
设椭圆 的左右焦点分别为
的左右焦点分别为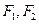 ,离心率
,离心率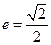 ,过
,过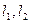 ,且
,且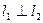 ,
,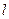 :
: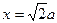 于
于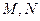 两点。
两点。 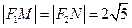 ,求 椭圆的方程;
,求 椭圆的方程;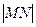 取最小值时,试探究
取最小值时,试探究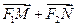 与
与
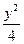 =1的交点为A、B,点P为椭圆上的动点,则使△PAB的面积为
=1的交点为A、B,点P为椭圆上的动点,则使△PAB的面积为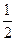 的点P的个数为( )
的点P的个数为( )